ワーシャルフロイド法
概要
ワーシャルフロイド法はグラフの最短距離を求めるアルゴリズムで、
隣接行列を使用して全ての頂点間の最短距離を調べて経路の検出を行います。
※グラフの用語が使用されているので頂点や辺、隣接行列など聞き覚えのない方は
こちらで確認していただければと思います。
最短経路アルゴリズムは他にベルマンフォード法やダイクストラ法があり、
実装の単純さではこのアルゴリズムが最も単純ですが、
計算量の多さから遅い部類に入るので余り実用的ではありません。
サンプル
サンプルはここからダウンロードできます。
環境については以下の内容となっています。
開発環境
| VSのバージョン |
| VisualStudio 2019 |
流れ
ワーシャルフロイド法を使って最短経路を見つける流れを説明します。
説明で使用するグラフは以下の図を使って最短経路を検出します。
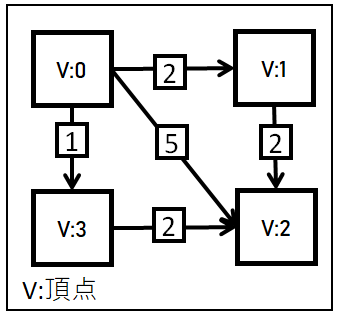
①.初期化
今回は行が始点、列が始点となっている行列を使用します。
各項目では始点と終点が隣接していたらコストを設定し、
始点と終点が同じ場合は0をそれ以外は、その意図を明示する値を設定します。
※今回の説明では「∞」を指定しています。
| 始/終 |
V0 |
V1 |
V2 |
V3 |
| V0 |
0 |
2 |
5 |
1 |
| V1 |
∞ |
0 |
2 |
∞ |
| V2 |
∞ |
∞ |
0 |
∞ |
| V3 |
∞ |
∞ |
2 |
0 |
②.始点と終点に経由点をはさんで比較する
ワーシャルフロイド法は始点と終点に別の隣接頂点を挟み、
そちらの頂点を経由したほうが距離が短くなるかどうかを検証します。
検証に使用する比較式は以下の通りです。
始点 => 経由点の距離 + 経由点 => 終点の距離 < 始点 => 終点の距離
例えば始点がV0、終点がV2に頂点V1を経由した経路させてみます。
隣接している頂点間の距離は以下の通りです。
| 関係性 |
頂点情報 |
距離 |
| 始点 => 終点 |
V0 => V2 |
5 |
| 始点 => 経由点 |
V0 => V1 |
2 |
| 経由点 => 終点 |
V1 => V2 |
2 |
この情報を比較式にあてはめます。
2 + 2 < 5
上の比較式の通り、直接よりも経由した方が距離が短くなったので、
こちらの経路を採用します。
採用した場合、先ほどの隣接行列の始点 => 終点の値を更新します。
今回の場合は始点V0、終点V2の距離が更新されます。
| 始/終 |
V0 |
V1 |
V2 |
V3 |
| V0 |
0 |
2 |
4 |
1 |
| V1 |
∞ |
0 |
2 |
∞ |
| V2 |
∞ |
∞ |
0 |
∞ |
| V3 |
∞ |
∞ |
2 |
0 |
③.全ての隣接頂点に対して②を行う
全頂点の最短距離を調べるには②で行った比較を全ての隣接頂点に対して行います。
以下の表は最短距離の最終結果です。
| 始/終 |
V0 |
V1 |
V2 |
V3 |
| V0 |
0 |
2 |
3 |
1 |
| V1 |
∞ |
0 |
2 |
∞ |
| V2 |
∞ |
∞ |
0 |
∞ |
| V3 |
∞ |
∞ |
2 |
0 |
この結果から始点と終点間の最短距離が分かります。
例えば先ほど②の比較で使用したV0からV2までの最短距離は3です。
また、V3からV0までの距離は∞になっているので移動不可であることも分ります。
実装方法
サンプルの一部を使って最短距離検出の説明したいと思います。
※コード量を少なくするために必要ではない部分は削ったり、
一部コードを変更しています。
最短経路検出は「流れ」の項目を実装するだけです。
まずは「①」の初期を行います。
// 距離格納用配列
int g_DistanceList[NodeNum][NodeNum];
void InitDistanceList()
{
// 初期値設定
for (int i = 0; i < NodeNum; i++)
{
for (int j = 0; j < NodeNum; j++)
{
if (i != j)
{
g_DistanceList[i][j] = Infinity;
}
else
{
g_DistanceList[i][j] = 0;
}
}
}
// 始点 => 終点間にコストを設定
for (int i = 0; i < NodeNum; i++)
{
for (int j = 0; j < NodeNum; j++)
{
for (int k = 0; k < EdgeNum; k++)
{
if (j == g_Edge[k].ToVertexId &&
i == g_Edge[k].FromVertexId)
{
g_DistanceList[i][j] = g_Edge[k].Cost;
break;
}
}
}
}
}
隣接行列は正方行列になるので、最短距離を格納する整数型や実数型の
2次元配列を用意して、各次元のサイズは頂点数にします。
その配列に対して「始点と終点が同じ」「隣接していない」
「隣接している」のどれかケースにわけて初期値を設定します。
| 条件 |
初期値 |
| 始点と終点が同じ |
0 |
| 隣接していない |
距離で設定されない値
※サンプルは10000 |
| 隣接している |
頂点間のコスト |
初期化が終了したら、②の比較処理を実装します。
// 始点 => 経由点 + 経由点 => 終点の距離が始点 => 終点の距離よりも小さいかチェック
if (g_DistanceList[始点][経由点] + g_DistanceList[経由点][終点] < g_DistanceList[始点][終点])
{
// 始点 => 終点の距離を更新
g_DistanceList[始点][終点] = g_DistanceList[始点][経由点] + g_DistanceList[経由点][終点];
}
最後の③実装で、上の比較処理が全ての頂点間で行われるようにします。
// 経由する頂点
for (int k = 0; k < NodeNum; k++)
{
// 始点
for (int i = 0; i < 1; i++)
{
// 終点
for (int j = 0; j < NodeNum; j++)
{
// 始点 => 経由点 + 経由点 => 終点の距離が始点 => 終点の距離よりも小さいかチェック
if (g_DistanceList[i][k] + g_DistanceList[k][j] < g_DistanceList[i][j])
{
// 始点 => 終点の距離を更新
g_DistanceList[i][j] = g_DistanceList[i][k] + g_DistanceList[k][j];
}
}
}
}
これで、ワーシャルフロイド法による最短経路検出が完了します。
最短距離を知りたい2頂点があったら、g_DistanceList[始点][終点]で確認可能です。
printf("%d => %dの最短距離は%d\n", start, goal, g_DistanceList[start][goal]);
実行結果:
0 => 2の最短距離は3
経路復元
上の説明は最短距離を検出する内容になっていますが、
最短経路には触れていないので、どの経路で行けば最短になるのか分かりません。
最短経路を調べるためには各頂点の最短距離を更新した頂点の番号を保存します。
保存は隣接行列と同じサイズの2次元配列を作成します。
配列の初期値は-1や始点番号などでプログラム上で認識しやすい値を設定しておきます。
以下の表は始点番号で初期化しています。
| 始/終 |
V0 |
V1 |
V2 |
V3 |
| V0 |
0 |
0 |
3 |
0 |
| V1 |
1 |
1 |
1 |
1 |
| V2 |
2 |
2 |
2 |
2 |
| V3 |
3 |
3 |
3 |
3 |
上の表で始点V0、終点V2の最短経路を求める場合は配列の[始点][終点]から始まり、
そこに設定されている要素が有効な値ならその値を2次元目の要素番号として使用します。
それを始点の値まで繰り返すと最短経路が求められます。
始点V0、終点V2の最短経路
0 => 3 => 2
この方法の実装ですが、距離の更新時に更新に使用した頂点を保存するだけです。
// 更新頂点保存用配列
int up_date_node_index[NodeNum][NodeNum];
for (int i = 0; i < NodeNum; i++)
{
for (int j = 0; j < NodeNum; j++)
{
up_date_node_index[i][j] = i;
}
}
// 経由する頂点
for (int k = 0; k < NodeNum; k++)
{
// 始点
for (int i = 0; i < 1; i++)
{
// 終点
for (int j = 0; j < NodeNum; j++)
{
// 始点 => 経由点 + 経由点 => 終点の距離が始点 => 終点の距離よりも小さいかチェック
if (g_DistanceList[i][k] + g_DistanceList[k][j] < g_DistanceList[i][j])
{
// 始点 => 終点の距離を更新
g_DistanceList[i][j] = g_DistanceList[i][k] + g_DistanceList[k][j];
// 終点距離を更新した頂点を保存
up_date_node_index[i][j] = up_date_node_index[k][j];
}
}
}
}
更新した頂点IDの配列が完成したらlistなどの機能を使用して、
終点の頂点IDから順番に始点までの頂点IDを保存していきます。
// 最短ルートを取得
int current_route_id = goal; // 今チェック中の経路ID
std::list shortest_route; // 経路保存用
shortest_route.push_front(goal);
while (true)
{
// 頂点配列から次の頂点IDを取得する
int next_id = up_date_node_index[start][current_route_id];
// 始点じゃなかったら追加
if (current_route_id != start)
{
shortest_route.push_front(next_id);
current_route_id = next_id;
}
else
{
break;
}
}
これで作成したリストから最短経路がわかります。
printf("最短ルートは");
for (int id : shortest_route)
{
printf("%d ", id);
}
printf("\n");
実行結果:
最短ルートは0 3 2
これで経路復元の実装も完了です。


