ベルマンフォード法
概要
ベルマンフォード法とはグラフの２頂点間の最短経路を求めるアルゴリズムで、
辺を主体として経路を割り出します。
※グラフの用語が使用されているので頂点や辺、隣接など聞き覚えのない方は
こちらで確認していただければと思います。
同じ最短経路アルゴリズムのダイクストラ法と比較されますが、
ベルマンフォード法は重みに負の値が使用されていても最短経路を導き出せます。
ただし、コストに負の値が含まれると負閉路が発生する可能性があるので、
負閉路を検出しなければいけません。
計算量
ベルマンフォードの最大計算量は「O(VE)」となっています。
Vは頂点の数、Eは辺の数です。
この計算量は負閉路を検出する時にも出てくるので覚えておいてください。
サンプル
サンプルはここからダウンロードできます。
環境については以下の内容となっています。
開発環境
| VSのバージョン |
| VisualStudio 2019 |
流れ
ベルマンフォードを使った最短経路検出の流れを以下のグラフで説明します。
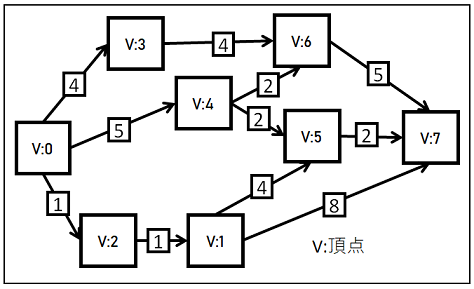
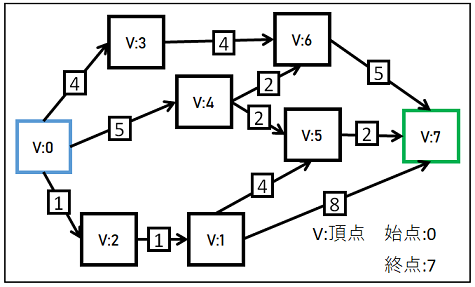
①．始点と終点を決める
まずは経路の始点と終点を決めます。
今回は始点が頂点０、終点が頂点７のパスの最短経路を見つけます。
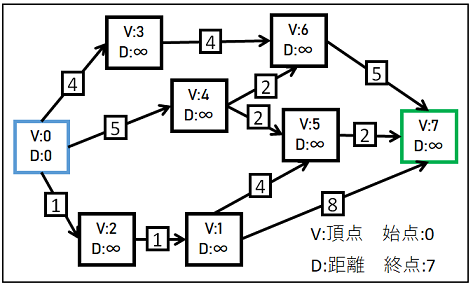
②．経路の距離を初期化する
始点と終点を決めたら次は各頂点までの距離を初期化します。
初期値は最短を求めるので小さい値は使用せず、
距離計算上で絶対にならないと確信が持てるほど大きい値を使用します。
※図では「∞」を使用しています。
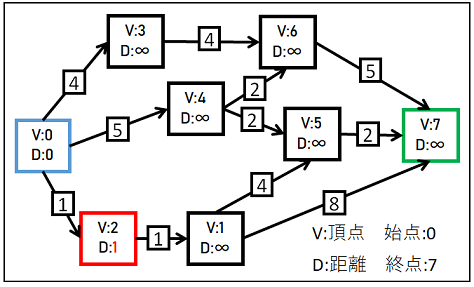
③．各頂点間の最短距離を調査する
初期化が終了したら、以下の条件式を使用して頂点間の最短距離を調査を行い
条件が成立したら隣接している頂点の最短距離を更新します。
基点となる頂点の最短距離 + 隣接頂点に到達するためのコスト < 隣接頂点の最短距離
例として頂点０と頂点２の２頂点間の調査を行います。
必要となる情報は以下の通りです。
| 頂点：0 |
最短距離：0 |
| 頂点0 => 頂点2の辺 |
コスト：1 |
| 頂点：2 |
最短距離：∞ |
この情報を式にあてはめます。
0 + 1 < ∞
条件は成立しているので頂点２の最短距離を基点の最短距離 + コストの値で更新します。
このように各頂点で最大値を設定しておき、その値を最短距離に置き換えていくことを
「
緩める」「
緩和」と呼ばれています。
④．全ての頂点間に対して③を行う
③で頂点０ => 頂点１までの最短距離の調査が完了したので、
同じ処理を全ての頂点間(辺)で行います。
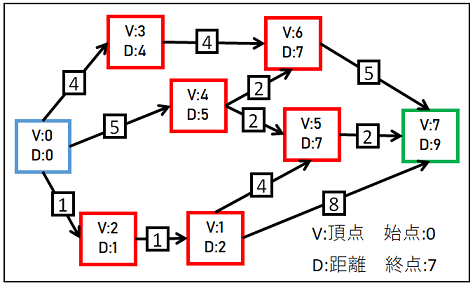上の図の頂点間の調査は頂点番号順に行っています。
(V0 => V1 => V2 => V3 => V4 => V5 => V6)
⑤．更新が行われなくなるまで④を行う
④を１度終了しただけでは最短距離が出たかわからないので
最短距離の更新が行われなくなるまで④を繰り返し行います。
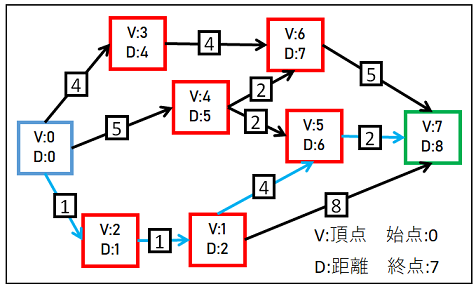上の図が最終的な頂点０ => 頂点７までの最短距離で、
最短ルートは「V0 => V2 => V1 => V5 => V7」でした。
負閉路の検出
概要でも書きましたが、ベルマンフォードの特徴は負のコストを扱えることです。
しかし、負のコストを扱う場合、「負閉路」が発生する可能性があります。
負閉路が発生した場合、目的地にたどり着けなかったり、
プログラムの処理次第では無限ループになったりするので、
しっかりと検出を行い、対策を立てる必要があります。
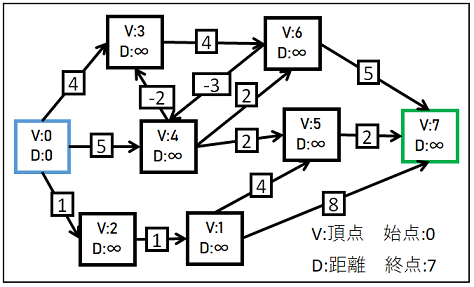負閉路用に先ほどのグラフの一部を変更しており、
V4 = >V3とV6 => V4に負のコストを追加しています。
負閉路の流れ
該当する辺だけ計算していますが、１度目の最短距離算出は以下のようになります。
(距離の調査の順番は頂点番号の小さい頂点の辺から順番に調べていると考えてください)
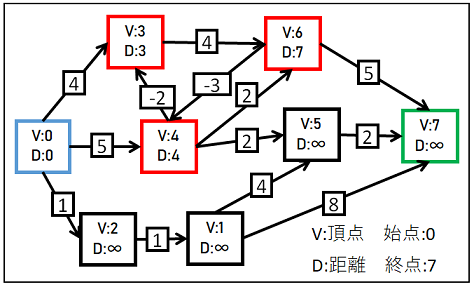
最短距離の調査(1回目)
| 番号 |
基点 => 隣接頂点 |
基点距離 |
コスト |
隣接頂点までの距離 |
条件式 |
結果 |
更新距離 |
| ① |
V0 => V3 |
0 |
4 |
∞ |
0 + 4 < ∞ |
更新 |
4 |
| ② |
V0 => V4 |
0 |
5 |
∞ |
0 + 5 < ∞ |
更新 |
5 |
| ③ |
V3 => V6 |
4 |
4 |
∞ |
4 + 4 < ∞ |
更新 |
8 |
| ④ |
V4 => V3 |
5 |
-2 |
4 |
5 - 2 < 4 |
更新 |
3 |
| ⑤ |
V4 => V6 |
5 |
2 |
8 |
5 + 2 < 8 |
更新 |
7 |
| ⑥ |
V6 => V4 |
7 |
-3 |
5 |
7 - 3 < 5 |
更新 |
4 |
２回目の最短距離調査は以下の通りです。
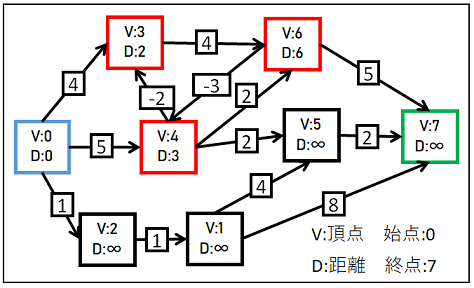
辺の調査(２回目)
| 番号 |
基点 => 隣接頂点 |
基点距離 |
コスト |
隣接頂点までの距離 |
条件式 |
結果 |
更新距離 |
| ① |
V0 => V3 |
0 |
4 |
3 |
0 + 4 < 3 |
非更新 |
3 |
| ② |
V0 => V4 |
0 |
5 |
4 |
0 + 5 < 4 |
非更新 |
4 |
| ③ |
V3 => V6 |
3 |
4 |
7 |
3 + 4 < 7 |
非更新 |
7 |
| ④ |
V4 => V3 |
4 |
2 |
3 |
4 - 2 < 3 |
更新 |
2 |
| ⑤ |
V4 => V6 |
4 |
2 |
7 |
4 + 2 < 7 |
更新 |
6 |
| ⑥ |
V6 => V4 |
6 |
-3 |
4 |
6 - 3 < 4 |
更新 |
3 |
３回目の最短距離調査は以下の通りです。
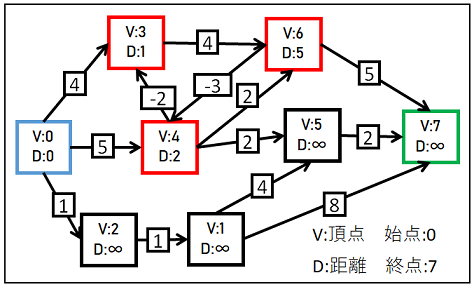
辺の調査(３回目)
| 番号 |
基点 => 隣接頂点 |
基点距離 |
コスト |
隣接頂点までの距離 |
条件式 |
結果 |
更新距離 |
| ① |
V0 => V3 |
0 |
4 |
2 |
0 + 4 < 2 |
非更新 |
2 |
| ② |
V0 => V4 |
0 |
5 |
3 |
0 + 5 < 3 |
非更新 |
3 |
| ③ |
V3 => V6 |
2 |
4 |
6 |
2 + 4 < 6 |
非更新 |
6 |
| ④ |
V4 => V3 |
3 |
-2 |
2 |
3 - 2 < 2 |
更新 |
1 |
| ⑤ |
V4 => V6 |
3 |
2 |
6 |
3 + 2 < 6 |
更新 |
5 |
| ⑥ |
V6 => V4 |
5 |
-3 |
3 |
5 - 3 < 3 |
更新 |
2 |
２回目と３回目の結果V3、V4、V6が１ずつ減っているのが分かります。
この流れを何回続けたとしてもこの法則が変わることはありません。
これが負閉路です。
検出方法
負閉路を検出は以下の条件で判断できます。
最短距離の更新が行われた &&
全ての辺の調査を何周したか == (頂点数 - 1)
上の条件が成立するということは、(頂点数 - 1)回目の調査中に
更新があったということになります。
この結果、最後の調査でも終わらなかったことが分かるので、
「条件成立 = 負閉路検出」と判断できます。
実装方法
最短距離検出と負閉路検出のコードをサンプルの一部を使って
説明したいと思います。
※コード量を少なくするために必要ではない部分は削っています。
最短距離検出
最短距離検出は「流れ」の項目にあったことを実装するだけです。
まずは「①」の経路の始点と終点を決めています。
void BellmanFord(int start, int goal)
BellmanFord関数の引数で始点と終点を決めます。
次に「②」の始点と始点以外の頂点の最短距離の初期化を行います。
int distances[NodeNum]; // 各頂点の最短距離保存用配列
// 各配列の初期化
for (int i = 0; i < NodeNum; i++)
{
distances[i] = Infinity;
}
// 始点の初期化
distances[start] = 0;
初期化が完了したら「④」の全ての頂点間の最短距離の調査を行います。
(③は④の一部として扱います）
for (int i = 0; i < EdgeNum; i++)
{
// 更新判断用エッジ(辺)を取得
Edge edge = g_Edge[i];
// エッジの始点の頂点の距離が更新済み
if (distances[edge.FromNodeId] != Infinity &&
// エッジの終点の頂点の距離が始点から距離よりも遠い
distances[edge.ToNodeId] > distances[edge.FromNodeId] + edge.Cost)
{
// 頂点までの最短距離を更新する
distances[edge.ToNodeId] = distances[edge.FromNodeId] + edge.Cost;
}
}
最後に「⑤」の調査中に更新がある限り繰り返す処理を実装して完成です。
// 更新がある限り繰り返す
while (true)
{
// ルート更新判定用
bool is_updated = false;
for (int i = 0; i < EdgeNum; i++)
{
// 更新判断用エッジ(辺)を取得
Edge edge = g_Edge[i];
// エッジの始点の頂点の距離が更新済み
if (distances[edge.FromNodeId] != Infinity &&
// エッジの終点の頂点の距離が始点から距離よりも遠い
distances[edge.ToNodeId] > distances[edge.FromNodeId] + edge.Cost)
{
// 更新があった
is_updated = true;
}
}
// 更新がなければ抜ける
if (is_updated == false)
{
break;
}
}
これで最終的にwhileを抜けた際にdistancesのgoal番目には
start番目の頂点からの最短距離が格納されています。
printf("最短距離は%d\n", distances[goal]);
実行結果：
最短距離は8
経路復元
上の説明は最短距離を検出するコードにはなっていますが、
最短経路には触れていないので、どの経路で行けば最短になるのか分かりません。
最短経路を調べるためには各頂点の最短距離を更新した頂点の番号を保存します。
上の図の各頂点の最後に距離の更新を行った頂点は次の通りです。
| 頂点番号 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
| 更新した頂点番号 |
-1 |
2 |
0 |
0 |
0 |
1 |
4 |
5 |
上の表を終点の頂点７から更新した頂点番号をたどっていけば
始点である０に到達します。
7 => 5 => 1 => 2 => 0
この方法をプログラムで実装する場合、最短距離を更新した頂点番号を
保存する配列を頂点の数だけ用意して、更新時に保存していきます。
int last_update_node_ids[NodeNum]; // 各頂点距離の最後に変更した頂点ID保存用
int distances[NodeNum]; // 各頂点の最短距離保存用配列
// 各配列の初期化
for (int i = 0; i < NodeNum; i++)
{
distances[i] = Infinity;
last_update_node_ids[i] = -1;
}
// 始点の初期化
distances[start] = 0;
for (int i = 0; i < EdgeNum; i++)
{
// 更新判断用エッジ(辺)を取得
Edge edge = g_Edge[i];
// エッジの始点の頂点の距離が更新済み
if (distances[edge.FromNodeId] != Infinity &&
// エッジの終点の頂点の距離が始点から距離よりも遠い
distances[edge.ToNodeId] > distances[edge.FromNodeId] + edge.Cost)
{
// 頂点までの最短距離を更新する
distances[edge.ToNodeId] = distances[edge.FromNodeId] + edge.Cost;
// 更新した経路の始点側の頂点IDを記録する
last_update_node_ids[edge.ToNodeId] = edge.FromNodeId;
}
}
更新した頂点IDの配列が完成したらlistなどの機能を使用して、
終点の頂点IDから順番に始点までの頂点IDを保存していきます。
// 最短経路を作成する
int current_route_id = goal; // 今チェック中の経路ID
std::list route_ids; // 経路保存用
route_ids.push_front(goal);
while (true)
{
// 頂点配列から次の頂点IDを取得する
int next_id = last_update_node_ids[current_route_id];
// 始点じゃなかったら追加
if (current_route_id != start)
{
route_ids.push_front(next_id);
current_route_id = next_id;
}
else
{
break;
}
}
これで作成したリストから最短経路がわかります。
printf("最短ルートは");
for (int id : route_ids)
{
printf("%d ", id);
}
実行結果：
0 => 2 => 1 => 5 => 7
負閉路検出
負閉路検出はHasNegativeLoopRoute関数で行っています。
int distances[NodeNum]; // 各頂点の最短距離保存用配列
for (int i = 0; i < NodeNum; i++)
{
distances[i] = 0;
}
// 頂点の数 * 辺の数だけ繰り返す
for (int i = 0; i < NodeNum; i++)
{
for (int j = 0; j < EdgeNum; j++)
{
Edge edge = g_Edge[j];
if (distances[edge.ToNodeId] > distances[edge.FromNodeId] + edge.Cost)
{
distances[edge.ToNodeId] = distances[edge.FromNodeId] + edge.Cost;
// ベルマンフォードは頂点数 * 辺の数が最大とされているので
// 最大値を回した状況でも更新があるのは負閉路があると判断する
if (i == NodeNum - 1)
{
return true;
}
}
}
}
上のコードのように最短距探索を最大計算量で実行し、
頂点数の繰り返し回数が(頂点数 - 1)の時に
最短距離の更新が発生していないかを調べれば負閉路検出ができます。
