アルゴリズムのグラフの基本
概要
グラフとは頂点と辺でデータの連結関係を表すデータ構造の事で、
頂点はノード、辺は枝やエッジとも呼ばれています。
グラフを図として表現すると以下のような内容になります。
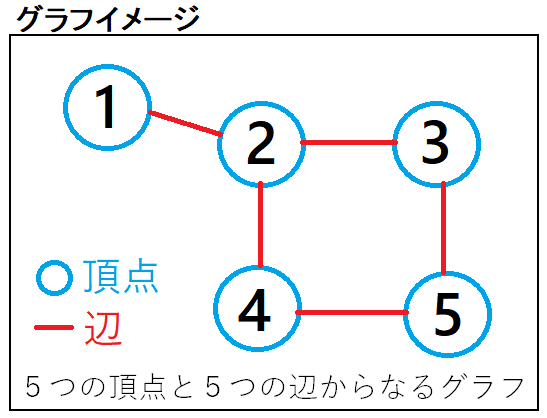頂点はデータ、辺はデータ間のつながりと考えます。
グラフの種類
グラフの種類には「有向グラフ」と「無向グラフ」があります。
有向グラフ
有向グラフは辺に対して向き(方向)があるグラフを指します。
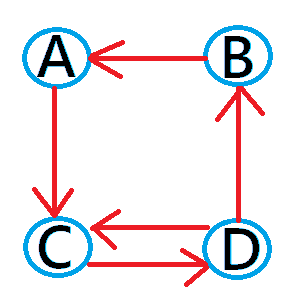上の図ではAとCの頂点間ではAからCに矢印が向いているのでアクセスが可能ですが、
CからAに対して矢印が向いていないのでアクセスできません。
このように有向グラフでは頂点間の辺の流れを示すことができます。
無向グラフ
無向グラフは辺に対して向き(方向)が無いグラフを指します。
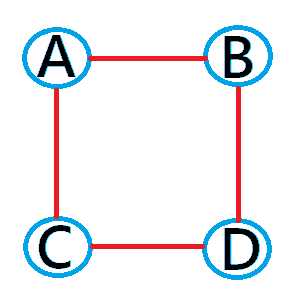上の図のように辺には矢印(方向)がないので、
片方からしかアクセスできないということはないので、
頂点間が双方向でアクセスできることを示しているとも考えられます。
用語
グラフには専門の用語がいくつかあるので以下で紹介したいと思います。
重み
重みとは辺に設定するコストのことです。
この重みは経路探索などで最短経路を算出するために使用されたりします。
コストには距離や時間、量などデータによって様々な情報が使われます。
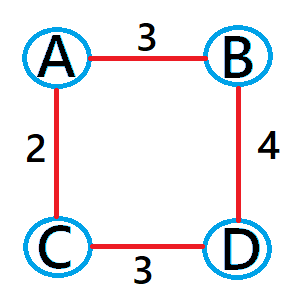上の図の辺の隣にある数字が重みです。
| 辺 |
重み |
| A => B間 |
3 |
| B => D間 |
4 |
| A => C間 |
2 |
| C => D間 |
3 |
隣接
隣接とは２つの頂点間に辺があることです。
パス
パスとは隣接している頂点の列のことです。
このパスの列の始まりの頂点の事を「始点」終わりの頂点を「終点」と呼んでいます。
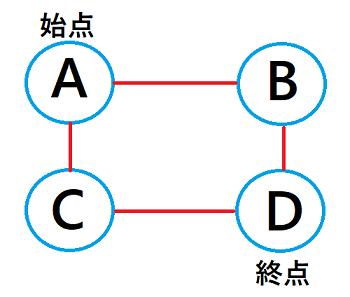上の図の場合のパスはこのようになります。
| パス |
| A => B => D |
| A => C => D |
閉路
閉路とは始点と終点が同じパスのことです。
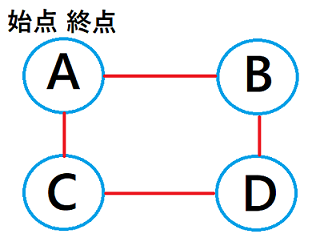上の図のようにAが始点であり終点となっているパスが閉路です。
この時のパスは以下の通りです。
| パス |
| A => B => D => C => A |
| A => C => D => B => A |
連結グラフ(連結)
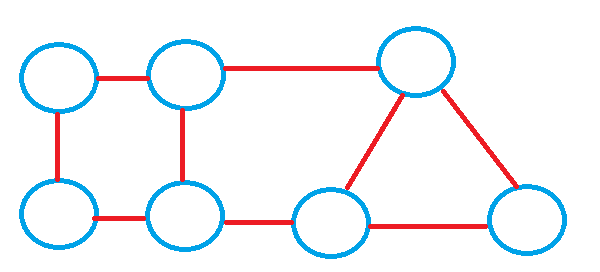
連結グラフとは任意の２頂点間にパスがつながっているグラフのことで、
全部つながっているグラフと考えても大丈夫です。
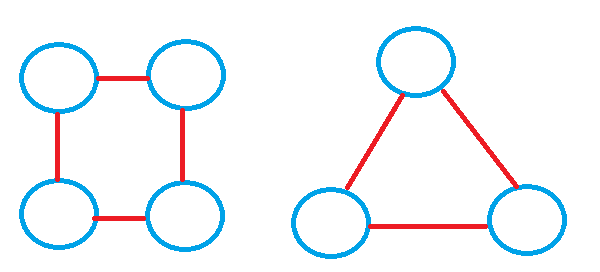
次のような連結がないグラフを非連結グラフと呼びます。
次数
次数とは１つの頂点から延びる辺の数です。
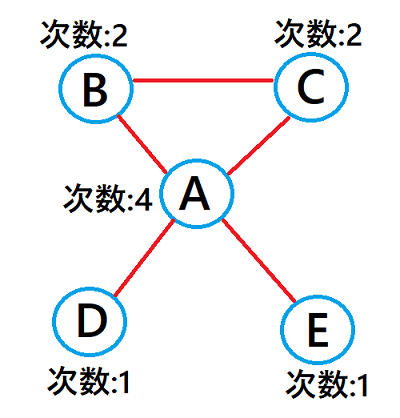上の図にあるように次数はこの通りです。
| 頂点 |
次数 |
| A |
4 |
| B |
2 |
| C |
2 |
| D |
1 |
| E |
1 |
木
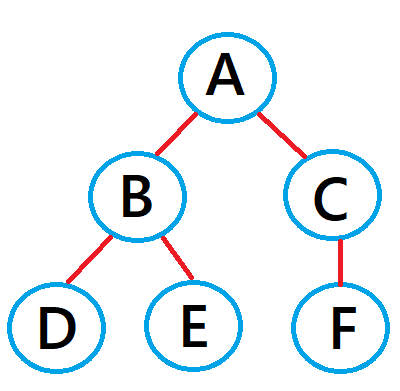
木とは閉路のない連結グラフのことで、
「辺の数が頂点の数-1」という特性があります。
森
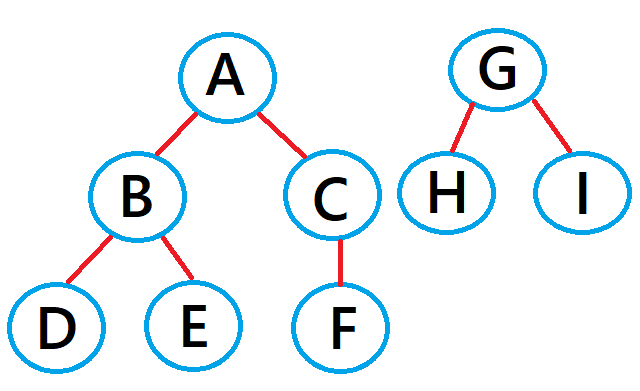
森とは閉路のない非連結グラフのことです。
グラフの表現
グラフの表現方法として有名なものは「隣接行列」と「隣接リスト」があります。
この方法のどちらかを使用すればデータをプログラムで表現できます。
隣接行列
隣接行列とは文字通りグラフを表すために行列を使用した表現方法です。
行列は頂点の数を縦と横に使用するので正方行列となり、
行が基点となる頂点、列が基点との関係を確認する頂点となります。
単純な隣接行列では繋がっているか、繋がっていないかなので、
繋がっていれば「１」や「true」繋がっていなければ
「0」や「false」を使います。
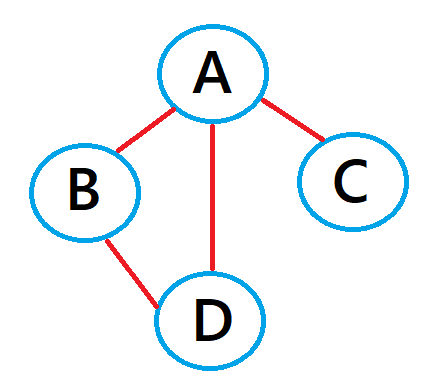今回のグラフは頂点数が４なので４×４の行列で
これを隣接行列にした場合はこのようになります。
| 基点/先 |
A |
B |
C |
D |
| A |
0 |
1 |
1 |
1 |
| B |
1 |
0 |
0 |
1 |
| C |
1 |
0 |
0 |
0 |
| D |
1 |
1 |
0 |
0 |
コード
以下は隣接行列をコードで表した場合の一例です。
struct Data
{
std::string Key;
};
const int MatrixNum = 4;
Data g_List[MatrixNum] =
{
{ "A" },
{ "B" },
{ "C" },
{ "D" },
};
/*
隣接行列
Aとつながりのある頂点 => B C D
Bとつながりのある頂点 => A D
Cとつながりのある頂点 => A
Dとつながりのある頂点 => A B
*/
bool AdjacencyMatrix[MatrixNum][MatrixNum] =
{
{ false, true, true, true },
{ true, false, false, true },
{ true, false, false, false },
{ true, true, false, false },
};
重み有り
重みがあるグラフの場合は隣接しているかの値を重みに変えます。
その際に繋がっていない頂点には重みで使用されない値を
設定するようにしてください。
例えば自然数が重みで設定されるなら、整数の最大値や負の数などです。
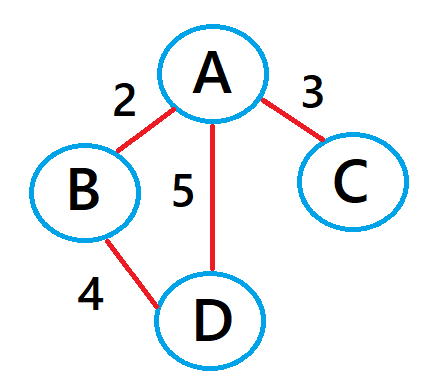上の重み付きのグラフを隣接行列に表すとこのようになり、
繋がっていない頂点間は「-1」を設定しています。
| 基点/先 |
A |
B |
C |
D |
| A |
0 |
2 |
3 |
5 |
| B |
2 |
0 |
-1 |
4 |
| C |
3 |
-1 |
0 |
-1 |
| D |
5 |
4 |
-1 |
0 |
隣接リスト
隣接リストは各頂点毎に隣接する頂点のリストを持っており、
それによって隣接状況を表現します。
隣接行列とは違って繋がっていない頂点を持たないので
使用するメモリ量を節約できます。
上の図を隣接リストで表すとこのようになります。
| 基点の頂点 |
繋がってる頂点 |
| A |
B C D |
| B |
A D |
| C |
A |
| D |
A B |
コード
以下は隣接リストのコードを表した場合の一例です。
// 頂点データ
struct Data
{
std::vector NodeList; // 隣接する頂点リスト
};
// グラフ
class Graph
{
public:
// 初期化
void InitData();
private:
std::map m_AdjacencyList; // 隣接リスト
};
void Graph::InitData()
{
// A頂点の隣接している頂点
m_AdjacencyList["A"].NodeList.push_back(&m_AdjacencyList["B"]);
m_AdjacencyList["A"].NodeList.push_back(&m_AdjacencyList["C"]);
m_AdjacencyList["A"].NodeList.push_back(&m_AdjacencyList["D"]);
// B頂点の隣接している頂点
m_AdjacencyList["B"].NodeList.push_back(&m_AdjacencyList["A"]);
m_AdjacencyList["B"].NodeList.push_back(&m_AdjacencyList["D"]);
// C頂点の隣接している頂点
m_AdjacencyList["C"].NodeList.push_back(&m_AdjacencyList["A"]);
// D頂点の隣接している頂点
m_AdjacencyList["D"].NodeList.push_back(&m_AdjacencyList["A"]);
m_AdjacencyList["D"].NodeList.push_back(&m_AdjacencyList["B"]);
}
