線分と円の当たり
概要
線分と円の当たり判定の説明を行います。
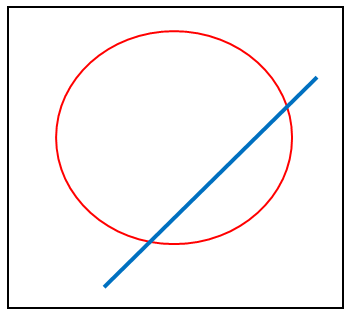レーザーなどの線分系のオブジェクトと円の当たりを持っているオブジェクトとの
当たり判定を行うときに有効です。
また、この判定方法は線分と矩形の当たり判定を行う際にも使用することがあります。
注意点
この記事内の座標軸はX軸「右が正、左が負」Y軸「下が正、上が負」で書いています。
サンプル
サンプルはここからダウンロードでき、環境については以下の内容となっています。
開発環境
| VSのバージョン |
DirectXのバージョン |
| VisualStudio 2019 |
DirectX9 |
判定の流れ
判定は以下の流れで行います。
| ①．必要なベクトルを用意する |
| ②．線分と円の中心の最短の長さを求める |
| ③．②の長さと円の長さの比較をする |
| ④．線分内に円があるかを調べる |
| ⑤．線分の末端が円の範囲内かを調べる |
①．必要なベクトルを用意する
まずは線分と円の情報を使用して必要なベクトルを用意します。
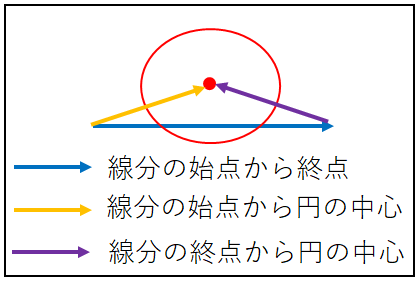
用意するベクトルは以下の通りです。
| 線分の始点から円の中心 |
| 線分の始点から終点 |
| 線分の終点から円の中心 |
メインで使用するのは上の二つのベクトルで最後の一つは④、⑤で使用します。
ベクトルの算出方法は
こちらでも書いていますが、二つの座標の終点側の座標から
始点側の座標を引くことで求めることができます。
②．線分と円の中心の最短の長さを求める
線分と円の中心の最短の長さは外積を使用することで求めることができます。
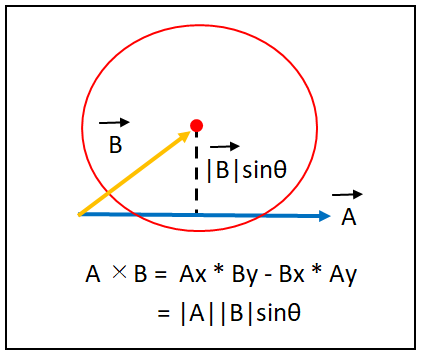上の図で円の外積を使用すれば円から線分に対して垂直な直線が延びています。
この直線の長さは線分の始点から円の中心までのベクトルの長さと
sinθの掛け算で求めることができます。
ですが、現在のある情報はベクトルだけなのでベクトルのなす角θが分かりません。
二つのベクトルがあるので、なす角を求めてから外積計算を行えますが、
そんなことしなくとも、もっと簡単に求めることができます。
まず、外積の式を見直してほしいのですが、外積は|A|と|B|とsinθの掛け算です。
その中で今回欲しい内容は「|B| * sinθ」なので、|A|が非常に邪魔です。
そこで、この|A|を邪魔にならないような値、掛けても結果が変わらない値、
つまり、単位ベクトルにします。
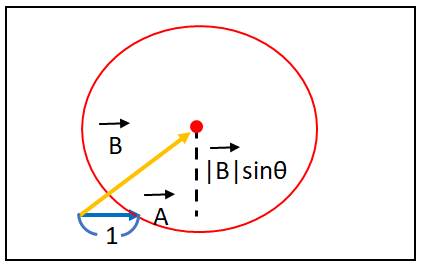上の絵のようにベクトルAを単位化することで、結果は「|B| * sinθ」となります。
今回欲しい結果は二つのベクトルの外積の結果ではなく、線分と円の最短の長さなので、
その結果が求められるのなら、このような値の変更は問題ありません。
これで答えが出るかというとそうでなく、相変わらずθの値が分かりません。
そこで、外積を求めるもう一つの式「Ax * By - Bx * Ay」を使用します。
こちらの式ならば、二つのベクトルの成分だけで求められます。
単位化したAとベクトルBを式「Ax * By - Bx * Ay」にあてはめて出た答えが
|B|sinθであり、線分と円の最短の長さです。
③．②の長さと円の長さの比較をする
②で線分と円の最短の長さが分かったら、その値を円の長さと比較します。
円の当たり判定は基本的に座標と円の半径の長さを比較して
半径の方が大きい値なら当たっていると判定します。
比較の結果、半径の方が大きいなら④に進みますが、半径の方が小さい場合は
当たっていないと判断してここで判定を打ち切ります。
④．線分内に円があるかを調べる
線と円の当たりなら③までで完結するのですが、線分の場合は
円が線分の範囲にあるかどうかを調べる必要があります。
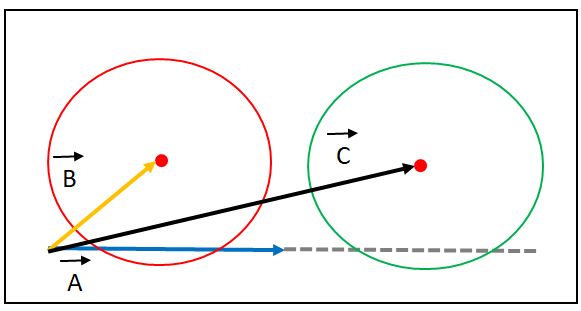上の絵のように赤の円は線分と交差していますが、緑の円は線分と交差していません。
ですが、どちらとも線分と円の長さは円の半径よりも短い結果となってしまうので、
線分の範囲に円があるかどうかを調べます。
調べる方法は内積の性質「鋭角は正の値、直角は0、鈍角は負の値」を利用します。
内積の定義は以下の通りです。
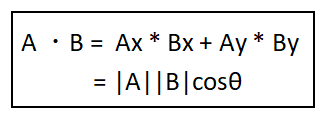この定義にそって以下の二つのベクトルから内積を求めます。
| ベクトルAの始点 |
ベクトルAの終点 |
ベクトルBの始点 |
ベクトルBの終点 |
| 線分の始点 |
線分の終点 |
線分の始点 |
円の中心 |
| 線分の始点 |
線分の終点 |
線分の終点 |
円の中心 |
円Aのように「
二つの結果(Aが鋭角、Bが鈍角等)が異なれば線分の範囲内」
円Bのように「
結果が同じ(A、Bともに鋭角 or 鈍角)場合は範囲外」です。
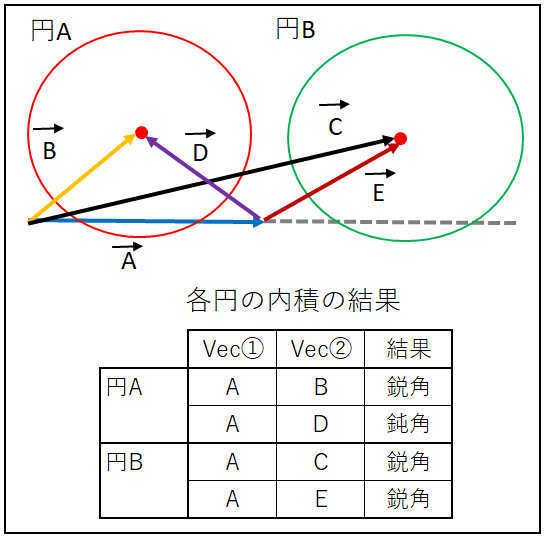
この内積の結果、線分が円の範囲内にあると判定したら
円と線分は当たっています。
もし、線分の範囲にないと判定されたら⑤に進みます。
⑤．線分の末端が円の範囲内かを調べる
線分の範囲に入ってないからといって当たっていないわけではありません。
以下のように線分の末端付近で当たっている可能性があります。
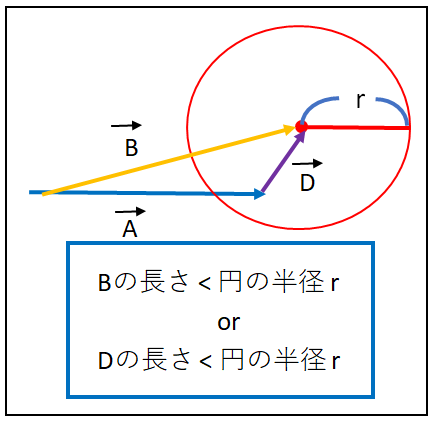
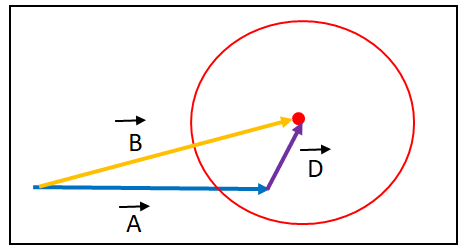この時に当たっているかどうかを判定する方法は各線分の末端である始点、終点と
円の中心の長さを求めて、その長さが半径よりも小さかったら当たりとします。
これで線分と円の当たり判定の流れは終わりです。
次は実装方法に移ります。
実装方法
実装は流れの内容を順番に実装していきます。
まず、①は線分と円から必要なベクトルを作成します。
// ベクトルの作成
Vec2 start_to_center = Vec2(circle.Position.X - line.Start.X, circle.Position.Y - line.Start.Y);
Vec2 end_to_center = Vec2(circle.Position.X - line.End.X, circle.Position.Y - line.End.Y);
Vec2 start_to_end = Vec2(line.End.X - line.Start.X, line.End.Y - line.Start.Y);
次の②でベクトルを線分の始点から終点のベクトルを単位化し、
そのベクトルと線分の始点と円のベクトルとで、外積計算を行い、
線分と円の最短の長さを算出します。
// 単位ベクトル化する
ConvertToNomalizeVector(normal_start_to_end, start_to_end);
/*
射影した線分の長さ
始点と円の中心で外積を行う
※始点 => 終点のベクトルは単位化しておく
*/
float distance_projection = start_to_center.X * normal_start_to_end.Y - normal_start_to_end.X * start_to_center.Y;
③では②の結果と円の半径を比較します。
// 線分と円の最短の長さが半径よりも小さい
if (fabs(distance_projection) < circle.Radius)
{
// 当たってる可能性あり
}
else
{
// 当たってる可能性なし
}
比較の結果次第で、当たっていないという結果で判定は終わります。
判定の結果、円の長さよりも小さかったら④に進んで、内積計算を行います。
// 始点 => 終点と始点 => 円の中心の内積を計算する
float dot01 = start_to_center.X * start_to_end.X + start_to_center.Y * start_to_end.Y;
// 始点 => 終点と終点 => 円の中心の内積を計算する
float dot02 = end_to_center.X * start_to_end.X + end_to_center.Y * start_to_end.Y;
// 二つの内積の掛け算結果が0以下なら当たり
if (dot01 * dot02 <= 0.0f)
{
return true;
}
最後に⑤の線分の始点、終点と円の中心の長さと半径の長さを比較します。
/*
上の条件から漏れた場合、円は線分上にはないので、
始点 => 円の中心の長さか、終点 => 円の中心の長さが
円の半径よりも短かったら当たり
*/
if(CalculationVectorLength(start_to_center) < circle.Radius ||
CalculationVectorLength(end_to_center) < circle.Radius)
{
return true;
}
ここまで線分と円の判定は終了なので、当たった判定になっていなのなら
線分と円は当たっていません。
