ベクトルの基礎
概要
ベクトルとは「向きと大きさ」を持っている量のことです。 数学的以外にも会話や文章でベクトルという言葉が使用されますが、 こちらも方向性や向きといった意味合いで使用されています。 ゲーム開発の3Dゲームを作るためにはベクトルを知らないとゲームを作れないと言われています。
基本
ベクトルは図のように向きと大きさを矢印で表現します。 矢印が向いている方向がベクトルの向きで矢印の長さが大きさを表しています。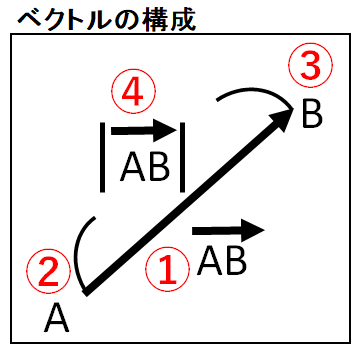
①.名前
ベクトルの名前は始点と終点をあわせたり別名をつけて、その上に→をつけます。
②.始点
始点とはベクトルの始まりのことです。 ベクトルの開始点は矢印が付いていない方を指します。
③.終点
終点とはベクトルの終わりのことです。 ベクトルの終点は矢印が付いている方を指します。
④.大きさ
大きさとはベクトルの始点から終点の長さで表現します。 矢印が長いほど向いている方向に力が大きく、短いほど小さいと考えます。 記述はベクトルの名前の左右に||をつけて表します。
ベクトルの計算
ベクトルでは加算、減算、実数倍、内積、外積などがあります。 今回は加算、減算、実数倍の説明をします。
加算
ベクトルの加算は左辺のベクトルの終点に右辺のベクトルの始点を合わせます。 この時の左辺ベクトルの始点から右辺ベクトルを終点を結ぶベクトルが加算の結果です。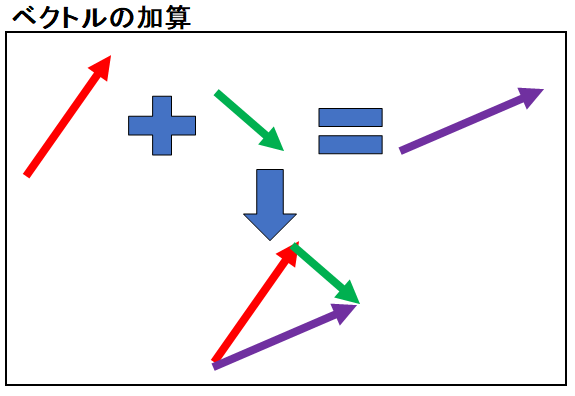
減算
ベクトルの減算は左辺のベクトルの始点と右辺のベクトルの始点を合わせます。 この時の右辺ベクトルの終点から左辺ベクトルの終点を結ぶベクトルが減算の結果です。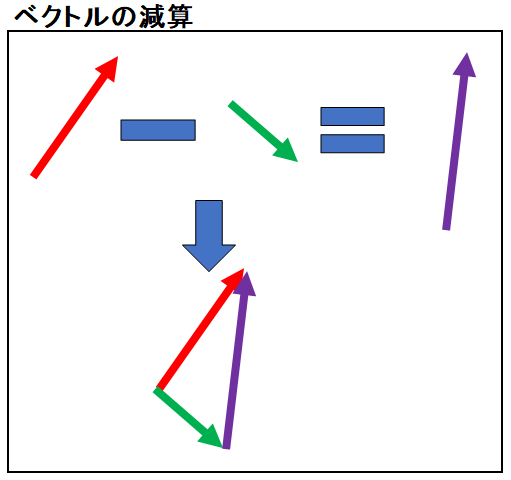
実数倍
実数倍は計算で使われたベクトルを実数の分だけベクトルを増やします。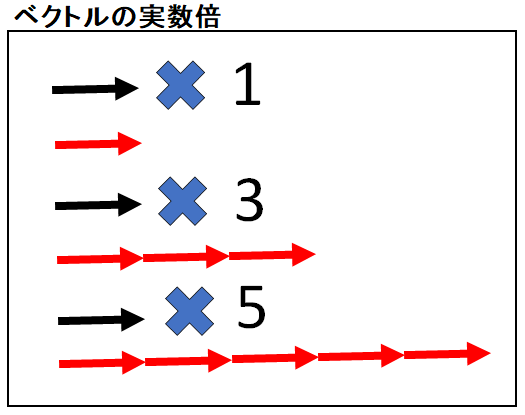
ベクトルの成分
ベクトルを座標軸で表現する場合は始点や終点を座標で表します。 この時のベクトルの始点から終点までの各軸の向きの値を「ベクトルの成分」と呼びます。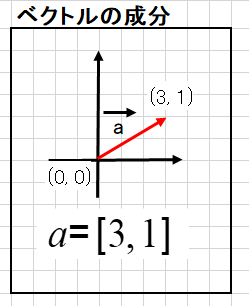
成分の表現方法
ベクトルの成分は「縦の数×横の数」で表し、縦に成分を記述する「列ベクトル」と、 横に成分を記述する「行ベクトル」があります。
列ベクトル
列ベクトルは縦がn、横が1で表現します。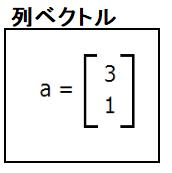
行ベクトル
行ベクトルは縦が1、横がnで表現します。
次数
列ベクトル、行ベクトルの成分の個数「n」のことを次数と呼び、 次数nのベクトルのことをn次元数ベクトルと呼びます。 例えば、行ベクトル(2, 1)は「2次元数ベクトル」です。
ベクトルの長さ(大きさ)
ベクトルは成分を使用することで長さを算出することができます。
例
二点間のベクトルの算出方法
ゲームなどではプレイヤーと敵、プレイヤーとカメラなど2つの座標から ベクトルを割り出すことが多々ありますので、算出方法を紹介します。
前提
ベクトル算出するには2つの座標で始点と終点をどちらにするかを決めます。
算出方法
算出方法は終点の座標から始点の座標を引くことで割り出すことができます。
式
2点間のベクトル = 終点の座標 - 始点の座標
例
・座標 プレイヤーの座標 => (x, y) = (20, 50) 敵の座標 => (x, y) => (40, 300) ・始点と終点 始点 => 敵の座標 終点 => プレイヤーの座標 ・計算 x成分 = プレイヤーの座標x(20) - 敵の座標x(40) y成分 = プレイヤーの座標y(50) - 敵の座標y(300) ベクトル => (x, y) = (-20, -250)
ベクトルの種類
ベクトルには特定の性質のものに名前がつけられています。
逆ベクトル
逆ベクトルはベクトルの大きさが同じで向きだけ真逆にしたベクトルのことです。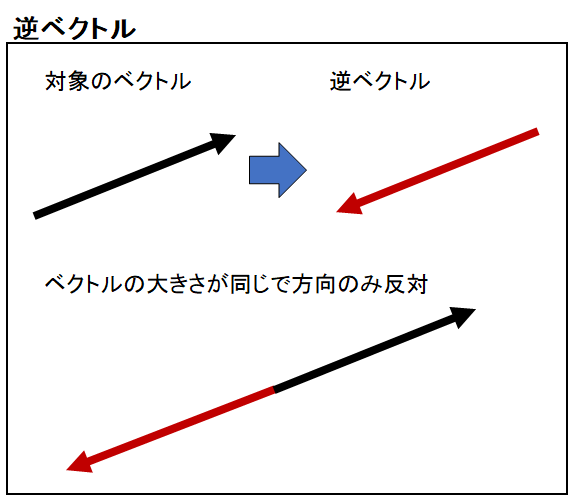
ゼロベクトル
ゼロベクトルとは始点と終点の位置が一致するベクトルのことです。 ゼロベクトルの大きさは「0」です。
例
始点 => (x, y) = (10, 40) 終点 => (x, y) = (10, 40) 2点間のベクトル x成分 = 10 - 10 y成分 = 40 - 40 ベクトル => (x, y) = (0, 0) 長さ => √0 * 0 + 0 * 0 => 0
単位ベクトル
単位ベクトルは大きさ1のベクトルです。 単位ベクトルについては下で詳細に説明します。
基本ベクトル
基本ベクトルとは各座標軸の正方向の成分が1で残りの成分が0のベクトルのことで、 X軸は(1, 0, 0)、Y軸が(0, 1, 0)、Z軸が(0, 0, 1)です。 基本ベクトルの長さは必ず1なので単位ベクトルです。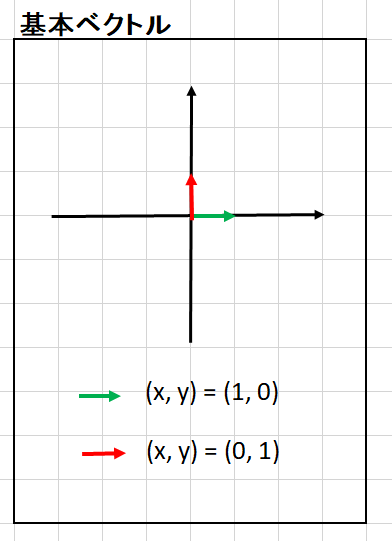
単位ベクトル
単位ベクトルとはベクトルの大きさが1のベクトルのことです。 単位ベクトルは大きさを1とすることでベクトルの方向情報のみにすることができます。 通常のベクトルを単位ベクトル化することを「正規化」と呼びます。
計算式
単位ベクトルは「各軸の量をベクトルの大きさで割る」ことで算出できます。
例
(X, Y) => (4, 3)のベクトルの正規化は以下の通りです。 ベクトルの大きさ => √4 * 4 + 3 * 3 => √25 => 5 x成分 => 4 / 5 => 0.8 y成分 => 3 / 5 => 0.6 単位ベクトル => (0.8, 0.6)
単位ベクトルの特性
単位ベクトルは向き情報のみを持っています。 正規化されていないベクトルは大きさの情報が含まれているので、 向き情報だけが欲しい場合は不要な情報が入っているといえます。 特定の位置からベクトルの向きに対して実数倍したい場合、 ベクトルの大きさが統一されていないと結果が異なることになります。
正規化をしてないベクトルを使った例
※以下で使うベクトルはわかりやすくするためにずらしてますが、 同じ位置にあると認識してください。 次の画像はどちらも同じ向きのベクトルですが、大きさが異なります。このベクトルを3倍した場合、当然2つのベクトルの結果は異なります。
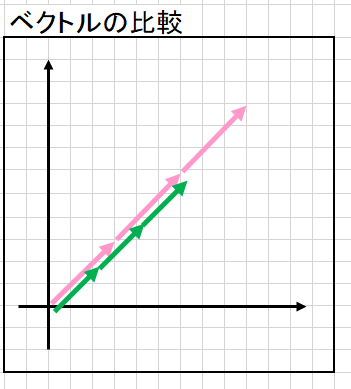
正規化したベクトル使った例
※以下で使うベクトルはわかりやすくするためにずらしてますが、 同じ位置にあると認識してください。 使用するベクトルは正規化していないベクトルの例で使ったベクトルです。このベクトルを次のように正規化すると向きと長さが同じになります。
正規化したベクトルを3倍にしても同じ結果になります。
このように正規化することで、計算によるずれがなくなります。


