木構造

概要

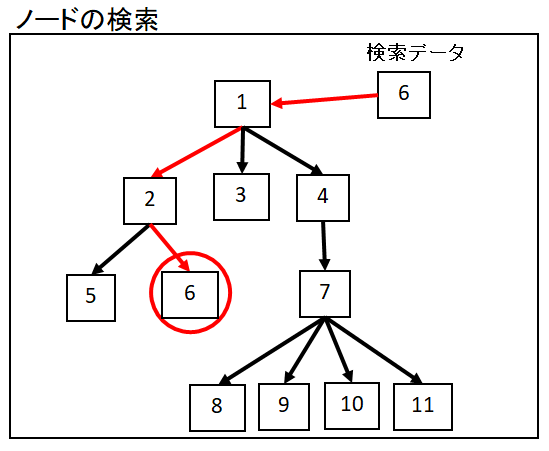
木構造とはグラフの一種で木の構造を模したデータ構造です。
閉路のない連結になっており、ノード数が枝の数よりも
必ず１つ少ないという特性を持っています。
※ノード、枝については「用語」の項目で説明します。

サンプル

こちらから木構造の簡易的なサンプルのダウンロードができます。
ノードの追加や検索方法などは簡単にしています。


	
開発環境
	

		
 言語 
		
 Visual Studio 
	
	

		
 C/C++
		
 Visual Studio 2017 

	

用語

木構造では専用の用語が使用されていますので、そちらを紹介したいと思います。
今回紹介する用語は「ノード」「枝」「ルート」「親子」「兄弟」「葉」です。

ノード

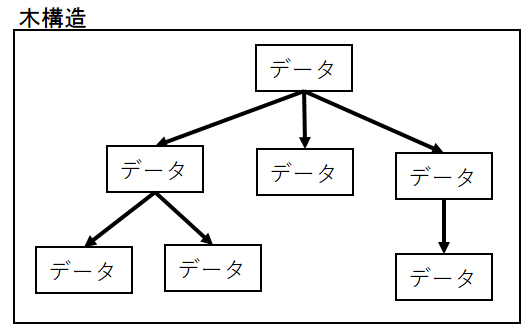
ノードとは木構造で管理するデータのことで、頂点と呼ばれることもあります。
ノードは自分の親、または子供を保存する領域を持っていることが多く、
その情報によって別のノードとつながり持つことができます。

枝

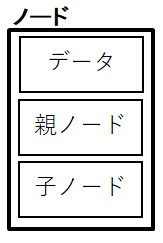
枝とはノード間をつなぐ線の事で、辺やエッジとも呼ばれています。
ノード内の親や子に別のノード情報が保存されることでノード間に枝が延びて、
ノード間に繋がりをもたせます。
グラフ的にもノードとノードの間に枝を繋ぐことで隣接していることを表します。

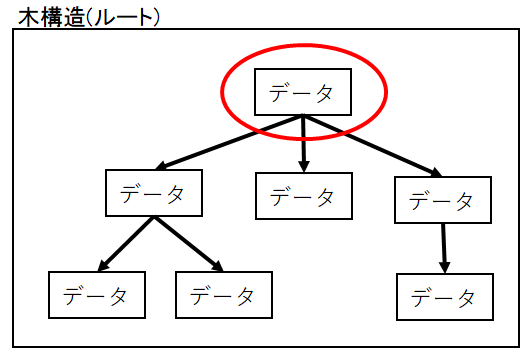
ルート

ルートとは木構造の最初のノードのことです。
木構造はこのルートから各ノード間のリンクが始まります。

親子

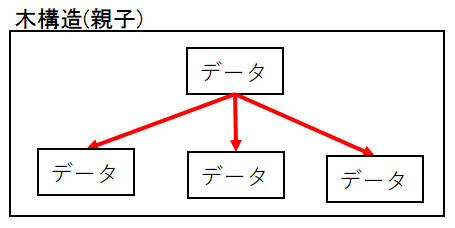
親子とはノードとノードがつながっている状態を指します。
ルートに近いノードを親、ルートから遠いノードを子とします。

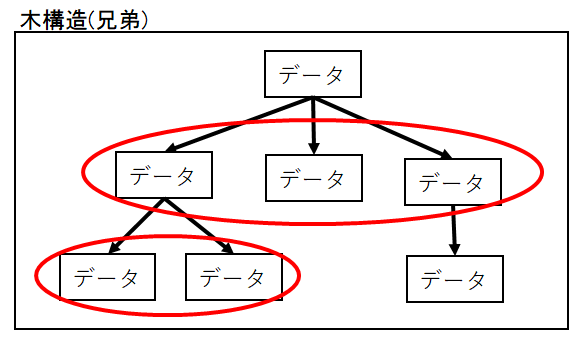
兄弟

兄弟とは同じ親をもつノードのことです。

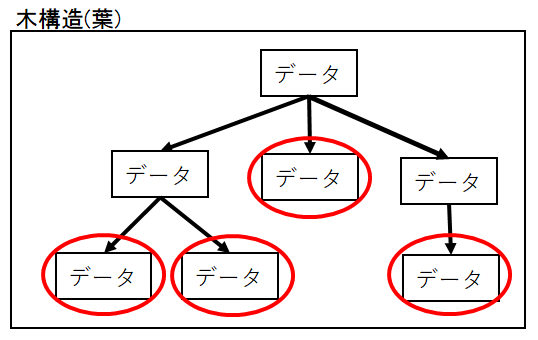
葉

葉とは木構造の末端にあるノードのことです。

必要な処理

木構造に必要な処理は「追加」「削除」「検索」の３つです。

追加

追加は指定したノードに対して新しいノードを追加します。
別の木構造のルートをノードとして追加することも可能です。

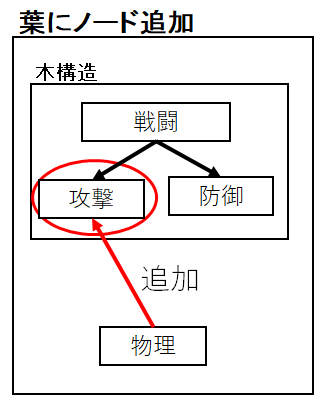
葉にノード追加

ノードの末端である葉に新しいノードを追加します。
次の画像では「攻撃」ノードに「物理」を追加しています。

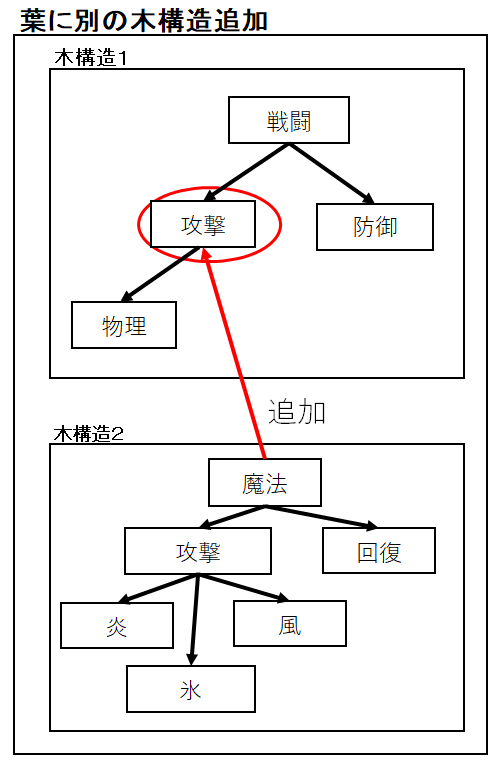
葉に別の木構造追加

ノードの末端の葉に別の木構造をそのまま追加します。
次の画像では「攻撃」ノードに「魔法」をルートとした木構造を
そのまま追加しています。

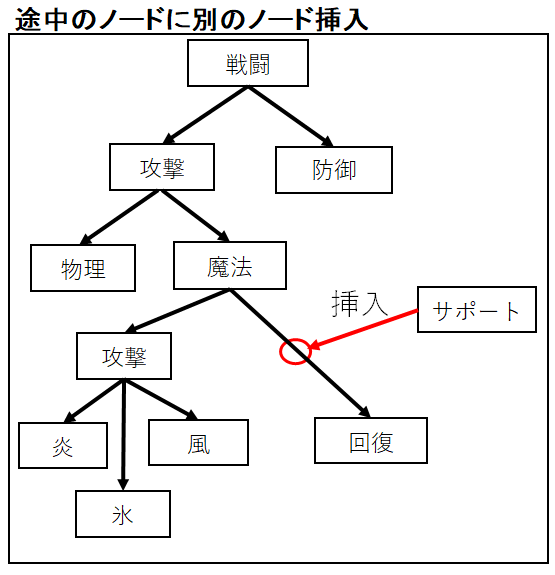
途中のノードにノード挿入

子供を持っているノードに別のノードを挿入します。
この時に挿入対象となったノードは挿入されたノードが新しい子になり、
挿入時に子だったノードの親が挿入されたノードになります。
次の画像では「魔法」と「回復」の間に「サポート」を挿入します。
その結果「魔法」の子が「サポート」、「回復」の親が「サポート」になります。

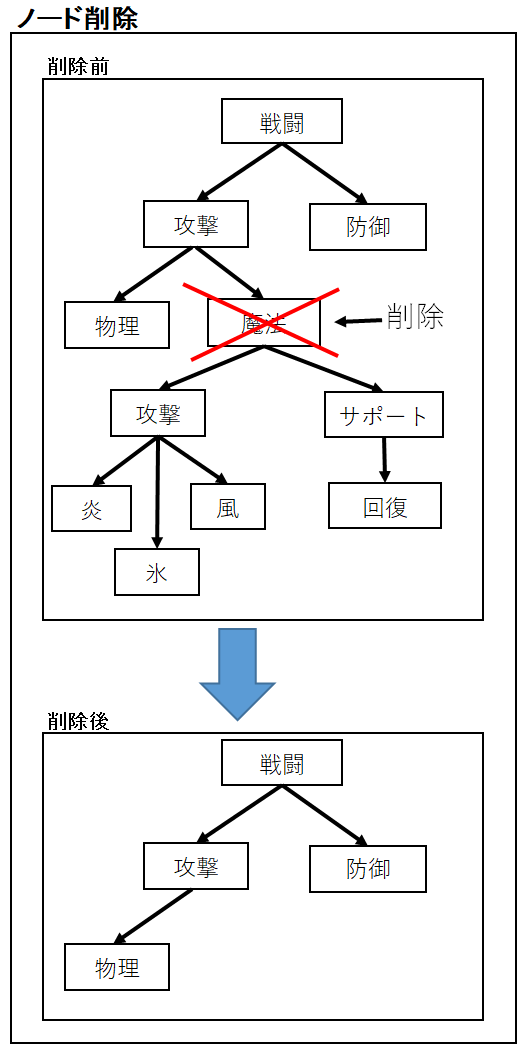
削除

削除は指定したノードをツリーの中から削除します。
木構造の種類にもよりますが、消されたノードの子供のノードもまとめて消すことが多いです。
次の画像では「魔法」のノードを消しますので、「魔法」以下のノードはすべて消去されます。
	

検索

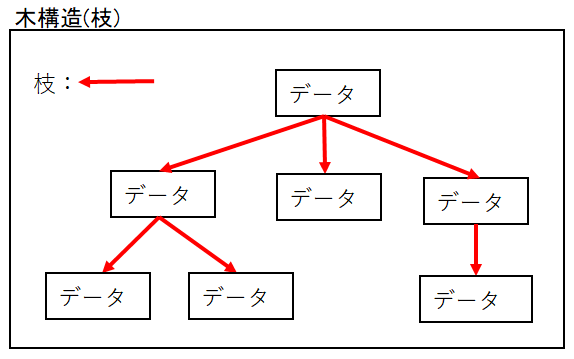
検索は指定したノードの情報を元にそのノードがあるかどうかを調べます。
基本的に検索する時はルートから始めます。
次の画像では「6」という値を木構造の中から検索しています。