2Dの外積の大きさは外積のZ成分

概要

最終更新日：2021/01/20

この記事は2Dの外積の大きさについて説明をしています。
主に次の項目に該当する方に向けて書いています。
※右手系で説明を行っています。

2Dの外積

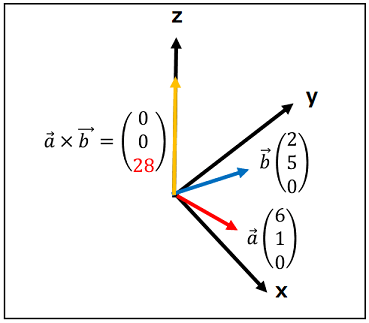
はじめに、外積は3Dベクトル同士を掛け合わせて新しいベクトルを算出する計算方法なので、2Dの外積は存在しません。
しかし、ゲームでは2Dのベクトルを使用して外積のベクトルの大きさを求めることがあり、
その際に「2Dの外積」や「2Dの外積の大きさ」といった表現を使っています。

2Dの外積を理解するためには以下のように普段の2DベクトルにZ成分0を加えた3Dベクトルで考えてください。

// 本来のベクトル
(x, y) = (6, 1) 
// Zが0の3Dベクトルとして考える
(x, y, z) = (6, 1, 0)

このようにZ成分を0としたベクトル同士で外積を行うと以下のような結果となります。



二つのベクトルのZ成分が0なので、外積結果のXとY成分は0となり、Z成分のみが残りました。
これは外積のベクトルがZ軸に対して平行なベクトルであることを指します。
そして、Z以外の成分が0なので、Z成分の値がベクトルの大きさであると言えます。

符号付きの大きさ

2Dの外積の結果である、Z成分の計算は負の値になることがあります。
つまり、ベクトルの大きさが負の値になるということなのですが、
大きさが負の値になることがあるのかというと外積の場合ならばありえます。
以下は外積のベクトルの大きさを求める式です。



この式のポイントはsinθが使われている事です。
sinθは「180°< θ < 360°」や「-180  < θ < 0°」など、角度によっては負の値となります。
そのため、絶対値にする計算を行わなかった場合、長さが負の値になることはありえるということです。
sinθを使用する式で外積の大きさを求めた際はこの点に注意して下さい。

長さが負になる角度

外積のsinθは二つのベクトルによって求められますが、この角度は次の法則で求められます。
「式の左側のベクトルを始線、右側のベクトルを動径として、始線から右回り or 左回りに回転する」
回転の方向は左手系か右手系かで決まります。
今回は右手系なので、左回りとなります。



上の図のように左側の外積ではaからbへ左回りで移動するとすぐに到達するため、角度は小さくてすみますが、
右側の外積では、aからbへ左回りで移動すると遠回りになるため、大きな角度が作られてしまいます。
このようにして180°を超えた角度は作られます。
そして、このような180°を超えた角度の場合、2Dベクトルの外積の大きさは負の値になります。

まとめ