度数法と弧度法(ラジアン)

概要

角度には「度数法」と「弧度法」という２種類の表記法があります。
一般的な社会でよく利用されているのが度数法で、弧度法はプログラムなどの計算で
使用する際によく利用されています。

度数法

度数法は角度を0～360の値で表現する方法です。
「～度」や「～°」と書き、「～ど」と読みます。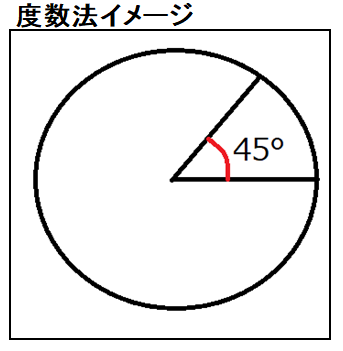

弧度法

弧度法とは円(扇)の弧の長さ(中心角の大きさの割合)を用いた
角度の表現方法のことです。
この弧度法で使用される単位はラジアンと呼ばれています。
プログラムで使用する計算では度数ではなく弧度法を用いて行うので
絶対に慣れておくべきです。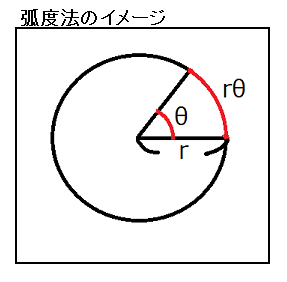



ラジアンの範囲
ラジアンは円の１周を2π(6.28....)で表します。
これはラジアンの値が弧の長さからきていること、
円周の長さが「直径 * 円周率」を求めること、
ラジアンは半径１の単位円で考えることを基本としているからです。

円周の長さ
2 * 3.14... => 6.28...

度数 ⇔ 弧度変換

度数法と弧度法は角度は計算で変換を行うことができます。
これらの計算もプログラムではよく利用するので覚えておいたが方がいいです。

弧度法(ラジアン) => 度数
弧度法(ラジアン)から角度への変換は以下の計算式で行います。
	
角度(ラジアン) * 180 / 円周率

例
6.28 * 180 / 3.14 => 360

3.14 * 180 / 3.14 => 180

度数 => 弧度法(ラジアン)
度数法から弧度法(ラジアン)への変換は以下の計算式で行います。

式
角度 * 円周率 / 180

例
180 * 3.14 / 180 => 3.14

360 * 3.14 / 180 => 6.28