円と円の当たり
概要
最終更新日:2020/03/03 円と円の当たり判定の方法について書いた記事です。 この記事は以下の内容を知りたい方に向けて書いています。
- 円と円の当たり判定の方法が知りたい
- 円と円の当たり判定の実装方法が知りたい
目次
円と円の当たり判定とは
円と円の判定は当たり判定の中で簡単な部類に入りますが、 シューティングの当たり判定や、処理コストの高い判定を行うかを判定するための 判定処理に使われるなど、ゲーム内で高頻度で使用されることが多い判定です。
判定方法
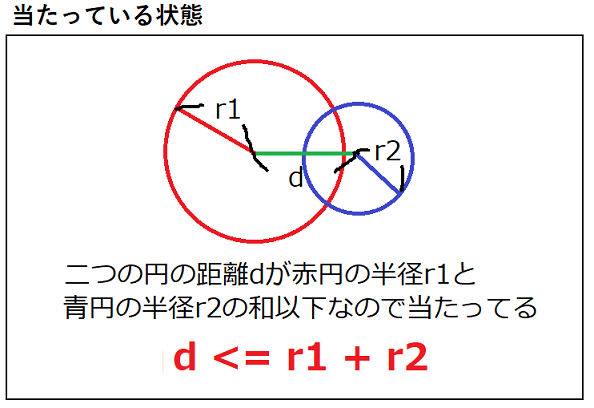
判定方法は二つの円の中心から距離を測り、その距離が二つの円の半径の和以下ならば 当たり、半径の和よりも大きければ当たっていないとなります。
当たってる
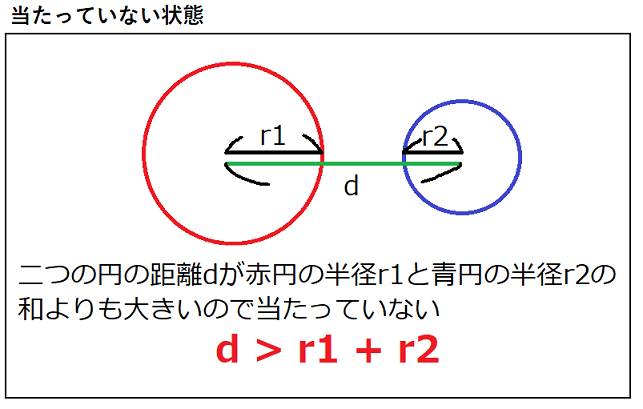
当たってない
計算方法
円の判定で必要となる計算は二つの円の距離の算出と半径同士の足し算です。 足し算は問題ないと思いますので、円の距離の算出方法のみを記述します。
2点間の距離を測る計算式
2点間の距離を測る計算式は以下のように単純な式となっています。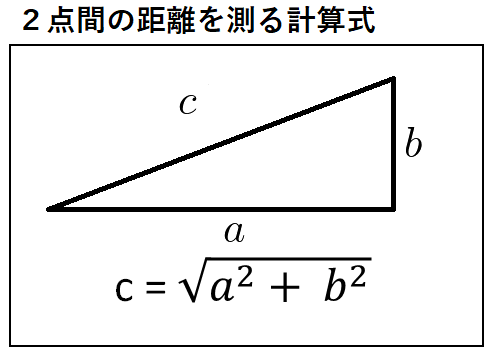
円の距離を測る
距離を測るには二つ円のX軸とY軸の長さが必要です。 これは片方の座標からもう一つの座標で引き算を行うことで求められるので、 赤円と青円の座標を以下のように考えます。この座標を2点間の距離を割り出す式に当てはめてます。
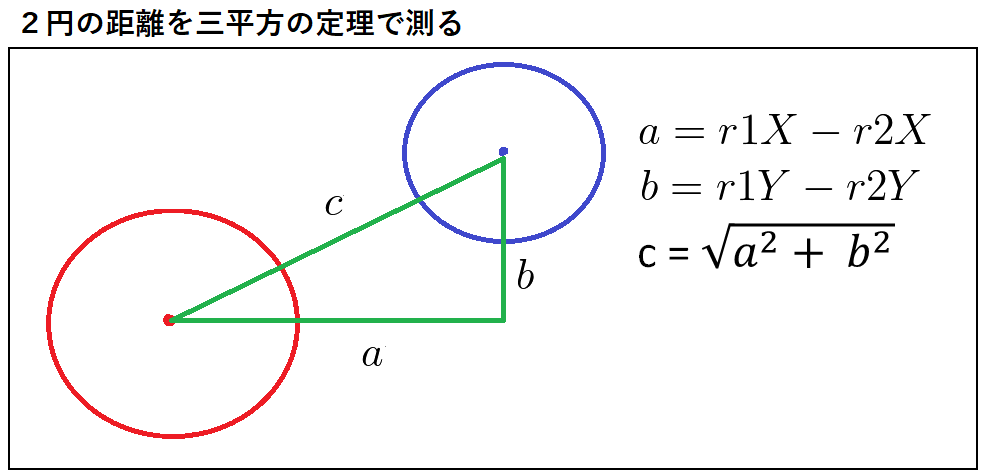
距離と半径の和を比較する
2点の座標を図る計算から二つの円の距離が算出されました。 この距離と二つの円の半径の和を比較して、距離の方が小さければ当たりと判断し、 大きければ当たってないと判断します。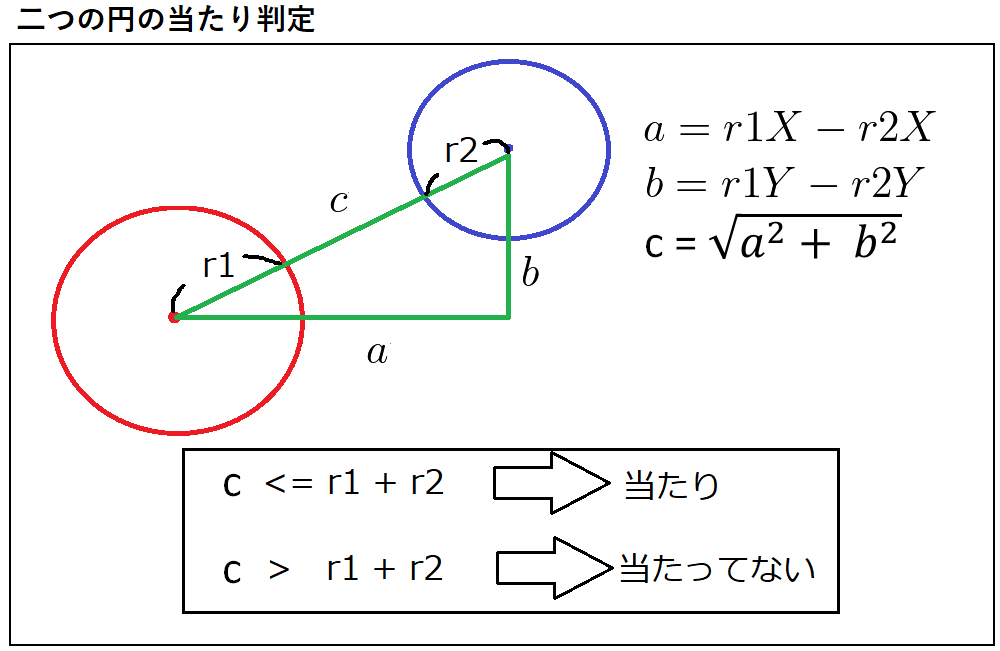
実装
以下でプログラムで実装する方法の例を紹介します。 ※紹介する実装方法が絶対ではありません。
単純な実装
プログラムで円の当たりを実装するには「円の座標(X、Yともに必要)」「半径」が
必要なので、それらを変数として用意して判定を行います。
#include <stdio.h>
#include <math.h>
void main(void)
{
// 円1の情報
float circle1_pos_x = 20.0f;
float circle1_pos_y = 40.0f;
float circle1_radius = 5.0f;
// 円2の情報
float circle2_pos_x = 25.0f;
float circle2_pos_y = 30.0f;
float circle2_radius = 8.0f;
float a = circle1_pos_x - circle2_pos_x;
float b = circle1_pos_y - circle2_pos_y;
float c = sqrt(a * a + b * b);
if (c <= circle1_radius + circle2_radius)
{
printf("a = %.2f b = %.2f c = %.2f\n", a, b, c);
printf("%.2f <= %.2f\n",
c,
circle1_radius + circle2_radius);
printf("当たってる\n");
}
else
{
printf("当たってない\n");
}
getchar();
}
当たり情報をまとめる
上の例では1つの円の当たり判定情報をのために変数を複数宣言していますが 判定はプレイヤー、弾、敵などの複数のオブジェクトで行うため、 その分だけ、変数宣言が必要となります。float player_pos_x; // プレイヤーの座標X float player_pos_y; // プレイヤーの座標Y float player_radius; // プレイヤーの半径 float enemy_pos_x[100]; // 敵の座標X配列 float enemy_pos_y[100]; // 敵の座標Y配列 float enemy_radius[100]; // 敵の半径配列 float bullet_pos_x[100]; // 弾の座標X配列 float bullet_pos_y[100]; // 弾の座標Y配列 float bullet_radius[100]; // 弾の半径配列上のコードのように、判定を行うオブジェクトの種類が増えるごとに わざわざ複数の変数を宣言しなくてはいけないのは非常に面倒です。 そこで、構造体やクラスにまとめることで変数宣言の手間を省きます。#include <stdio.h> #include <math.h> // 円データ typedef struct { float m_PosX; // X座標 float m_PosY; // Y座標 float m_Radius; // 半径 } Circle; void main(void) { // 円1の情報 Circle circle1 = { 20.0f, 40.0f, 5.0f }; // 円2の情報 Circle circle2 = { 25.0f, 30.0f, 8.0f, }; float a = circle1.m_PosX - circle2.m_PosX; float b = circle1.m_PosY - circle2.m_PosY; float c = sqrt(a * a + b * b); float sum_radius = circle1.m_Radius + circle2.m_Radius; if (c <= sum_radius) { printf("a = %.2f b = %.2f c = %.2f\n", a, b, c); printf("%.2f <= %.2f\n", c, sum_radius); printf("当たってる\n"); } else { printf("当たってない\n"); } getchar(); }構造体でまとめた方が宣言している箇所がすっきりします。
関数化する
当たり判定は様々な場所で使用する可能性があります。 その時に毎回上のコードを書いていたら大変手間です。 なので、関数化しておいて簡単に使えるようにしておいた方が作業時間を短縮できます。
| 関数内容 | circle1とcircle2のデータを使用し、 当たり判定チェックをする この判定で二つの円が当たっていればtrue、 当たっていなければfalseを返す |
|---|
| 戻り値 | bool型で当ったていればtrue、 当たっていなければfalseを返す |
|---|
| 引数の型 | 説明 |
|---|---|
| Circle circle1 | 判定用円データその1 |
| Circle circle2 | 判定用円データその2 |
定義
bool OnCollisionCircle(Circle circle1, Circle circle2)
{
float a = circle1.m_PosX - circle2.m_PosX;
float b = circle1.m_PosY - circle2.m_PosY;
float c = sqrt(a * a + b * b);
float sum_radius = circle1.m_Radius + circle2.m_Radius;
if (c <= sum_radius)
{
return true;
}
return false;
}
使用例
#include <stdio.h>
#include <math.h>
// 円データ
typedef struct
{
float m_PosX; // X座標
float m_PosY; // Y座標
float m_Radius; // 半径
} Circle;
bool OnCollisionCircle(Circle circle1, Circle circle2)
{
float a = circle1.m_PosX - circle2.m_PosX;
float b = circle1.m_PosY - circle2.m_PosY;
float c = sqrt(a * a + b * b);
float sum_radius = circle1.m_Radius + circle2.m_Radius;
printf("a = %.2f b = %.2f c = %.2f\n", a, b, c);
printf("%.2f <= %.2f\n", c, sum_radius);
if (c <= sum_radius)
{
return true;
}
return false;
}
void main(void)
{
// 円1の情報
Circle circle1 = {
20.0f,
40.0f,
5.0f
};
// 円2の情報
Circle circle2 = {
25.0f,
30.0f,
8.0f,
};
if (OnCollisionCircle(circle1, circle2) == true)
{
printf("当たってる\n");
}
else
{
printf("当たってない\n");
}
getchar();
}
高速化
円と円の当たり判定は若干ですが、処理速度を速めることができます。
それはsqrt関数を使用しないことです。
sqrtは平方根を求める関数で、距離を正確に求めるためには必要な計算ですが、
パフォーマンスが良い関数とは言えません。
この当たり判定では正確な距離ではなく、半径の和とどちらが
大きいかの比較で使用するだけなので以下のように変更しても問題ありません。
float a = circle1.m_PosX - circle2.m_PosX;
float b = circle1.m_PosY - circle2.m_PosY;
float c = a * a + b * b;
float sum_radius = circle1.m_Radius + circle2.m_Radius;
if (c <= sum_radius * sum_radius)
{
return true;
}
上の例ではsqrtは使用せず、半径の和を2乗しています。
このような方法でも問題なく判定は行えます。
これでsqrtを使用しなくなったので、処理コストが軽減します。