プロジェクション座標変換

■プロジェクション座標変換

プロジェクション座標変換はカメラの設定を行い
カメラに映る映像を決めるために行われる座標変換のことです。
カメラの設定は投影方法、前後のクリップ面の範囲、画角、アスペクト比の設定をします。

●投影方法
	平行投影：
		平行投影はオブジェクトが距離の影響を受けません。
		同じサイズのオブジェクトがあった場合、
		距離に関係なく同じサイズとして扱われます。
	
		

	透視投影：
		透視投影はカメラとオブジェクトの距離でサイズが変わります。
		オブジェクトがカメラに近ければ大きく、遠ければ小さくなります。
		
		
			
	以下は透視投影のイメージとなります。
	
		

	視錐台はカメラに映る範囲を表した空間で、平行投影は長方形
	透視投影は台形になります。
	
●投影に必要な情報
	クリップ面の範囲：
		クリップ面の範囲を設定することで視錐台のZ軸方向の映る範囲を決めます。
		手前を前面クリップ面、またはnear、奥行きを後方クリップ面、farと呼びます。

	画角：
		画角を設定することで視錐台のX軸とY軸の映る範囲を決めます。
		視野角ともよばれています。
		
	
	アスペクト比：
		投影する空間の縦横の比率です。
		基本的にウィンドウのサイズを使用します。

■変換行列の作成方法

プロジェクション座標変換の透視投影行列は以下の内容を使用しますので
この行列の各要素について説明をしたいと思います。

	
	
①．ScaleY：
	
		
	ScaleYは画角による拡縮の値になります。
	計算式は1 / tan(angle / 2)です。
	画角を2で割っているのは図にあるとおり画角はZ軸が中心になります。
	この性質を利用し、三角関数のtanを使用することで-1～1の値を算出し、
	その値を拡縮に利用しています。

②．ScaleX：
	ScaleXはScaleYと基本同じ原理です。
	異なる点があるのはアスペクト比で除算しています。
	これは縦横1:1の画面を例えば画面を横長にした場合
	そこに映っている内容は横長に映ってしまいます。
	それを解消するためにアスペクト比で除算しており、
	これで横長になっていた内容が元のサイズに戻ります。

③．ScaleZ：
	ScaleZは④と⑤に関連しており、クリップ面の距離の割合を拡縮率として利用しています。
	最後にfarによる乗算をおこなっていますが、これは最終的にzの範囲が
	クリップ空間の0～1の範囲かどうか確認するために必要なので行われています。
	
④．TransZ：
	TransZはnearの位置をクリップ空間の「z = 0」の位置にするための移動値になります。
	こちらも③と同じようにfarによる乗算をおこなっていますが、
	理由も③と同じでzの範囲をクリップ空間の0～1の範囲か確認するために
	必要なので行われています。

⑤．1：
	・1の理由：
		今までの行列ではここの部分は常に0だったと思います。
		なのになぜ今回は1が入っているかというとベクトルZの値をWの値に設定するためです。
		例えば (x, y, z, w)と通常の行列で計算を行った場合(x', y', z', 1)ですが、
		今回の行列を使用した場合は(x', y', z', z)となります。
		なぜwの部分にzをあてはめるようなことをするのかというと
		z値による拡縮を行うためです。
		透視投影行列はオブジェクトが手前に来るほど大きく、
		奥に行くほど小さく表示されますが、
		①～④までの計算にはZの値は使われておらず、
		距離による拡縮は行われていません。
		なぜ行列の中にzが使用されていないのかというとzの値は不定だからです。
		アスペクト比や画角は定数と扱えますがzの値は変わりますので
		あえてはずしてあります。

	・wの役割
		wがどのような場所で使用されているのかというとGPUで使用されています。
		GPUが変換後のx、y、z成分をw成分で除算してw = 1になるようにしています。
		
			例：
				(x, y, z, w) => (x / w, y / w, z / w, w / w)
		
		この性質を利用し、zの値をwに設定することでfarに遠ければ小さくなっていき、
		近ければ近いほど大きくなっていきます。

	・zの範囲チェック
		③と④でfarを乗算しているのもwの性質を利用しているからです。
		これによってzの値がnearだったら0、farだったら1となり、
		クリップ空間内に存在するかどうかを確認することが可能になります。

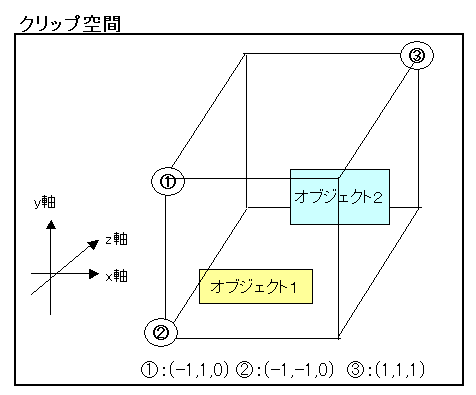
■クリップ空間

クリップ空間はプロジェクション座標変換によって作成された空間のことです。
空間の範囲はx=-1～1、y=-1～1、z=0～1になっており、この範囲の中にあるオブジェクトが
次のスクリーン座標変換で画面に表示されます。