論理演算の基本

概要

最終更新日：2020/02/15

論理演算の基本的な説明を書いた記事です。
主に次の項目に該当する方に向けて書いています。

コンピュータの基礎を知りたいと考えている方やITパスポートや基本情報技術者試験の
資格取得を目指している方のお役に立てたら幸いです。

論理演算とは

論理演算とは命題の真(true)と偽(false)の値を使用した演算の事です。
命題とは「AとBは等しい」や「x > y」などの真偽(正誤)が明確な文章や条件式です。
この命題の真偽には集合が使われています。

集合

集合とは条件によってグループ分けできるものの集まりです。
例えば下の図は職業がプログラマーという条件を満たしたの人たちの集合です。



この集合が複数集まっている状態の関係を表している図のことを
「ベン図」と呼んでいます。



上のベン図では職業がプログラマーとデザイナーの集合があり、
二つの集合の一部が重なっています。
これは二つの集合で共通の条件(例えば給与が一定額以上等)が
満たされているということです。
この二つ集合の共通部分を「共通集合」と呼びます。

論理演算の種類

論理演算の種類は基本が三種、複合が三種あります。

論理和

論理和は対象が二つの集合のどちらかの集合に当てはまったら真とする演算です。
表現としては「OR」「∨(または)」と書きます。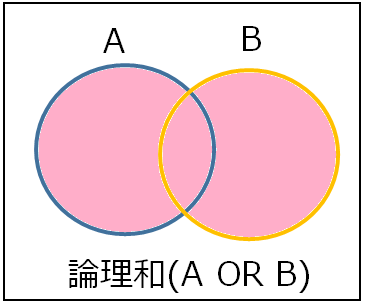

論理積

論理積は対象が二つの集合の共通集合に当てはまったら真とする演算です。
表現は「AND」「∧(かつ)」と書きます。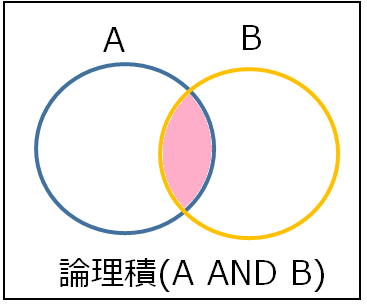

論理否定

論理否定は一つの集合で演算を行い、対象が集合ではなかったら真とします。
表現は「NOT」「¬(ではない)」と書きます。

排他的論理和

排他的論理和は論理否定、論理和、論理積を全て複合した演算で、
対象が共通集合以外の集合だったら真とします。
表現は「XOR」や「」「」と書きます。

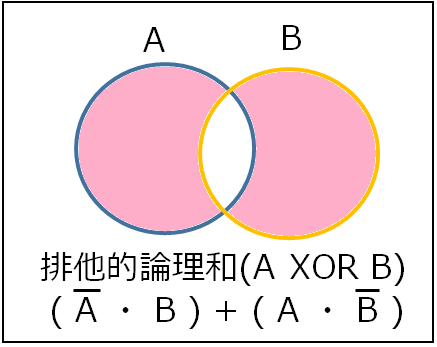
否定論理和

否定論理和は論理和を否定する演算で、
対象が二つの集合以外だったら真とします。
表現は「NOR」と書きます。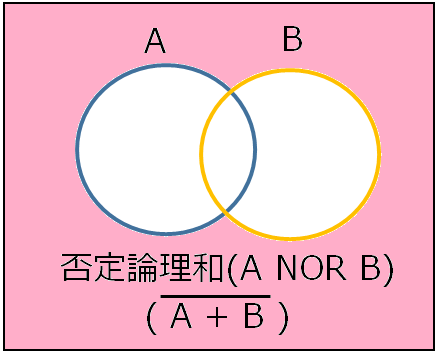

否定論理積

否定論理積論理積を否定する演算で、対象が共通集合以外
(集合以外を含む)だったら真とします。
表現は「NAND」と書きます。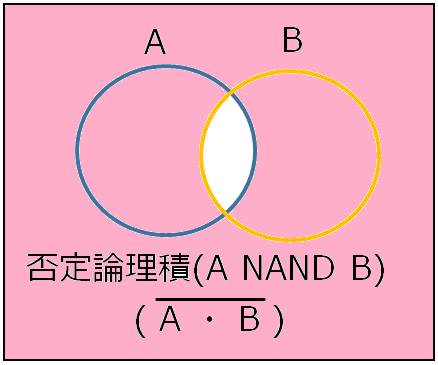

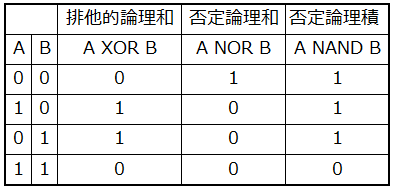
真偽値表

真偽値表とは各論理演算の入力と出力の関係を表現する表です。
表の値は「真と偽」か「1と0」で表現されます。
まずは、基本論理演算の真偽値表です。



次は、複合論理演算の真偽値表です。

ド・モルガンの法則

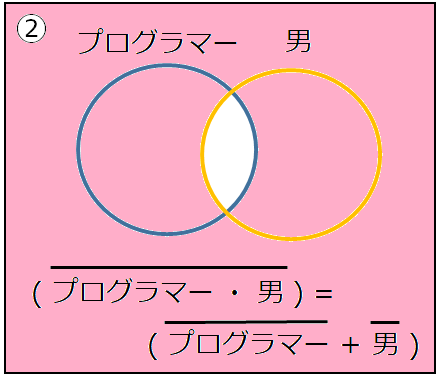
ド・モルガンの法則とは論理積、論理和の否定の関係を示した法則で、
以下のような関係式が成り立ちます。



この法則を「A：職業」「B：性別」として「プログラマーの男」で考えます。
①の式では論理和の否定が行われているので、
「プログラマーの男」は「プログラマーではない、または男ではない」となります。
そして、右辺では各集合の否定に対して論理積を行っているので、 
「プログラマーではない」かつ「男性ではない」というのは「別の職種の女性」です。
つまり、「プログラマーではない、または男ではない」は「別の職種の女性」を指しています。



②の式では論理積の否定が行われているので、
「プログラマーの男」は「プログラマーではない男」です。
そして、右辺では各集合の否定に対して論理和を行っているので、
「プログラマーではないまたは、男性ではない」というのは
「別の職種か性別が女性」となります。
つまり、「プログラマーではない男」は「別の職種か性別が女性」を指しています。

まとめ

今回の記事の要点を最後にまとめました。