2進数の四則演算

概要

最終更新日：2020/02/17

2進数の四則演算の説明を書いた記事です。
主に次の項目に該当する方に向けて書いています。

足し算

2進数の足し算は桁上がりの数字を注意すれば10進数の足し算と違いはありません。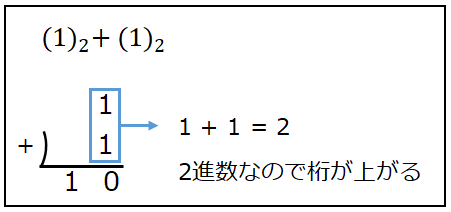




コンピュータの場合、8桁、16桁、32桁など、保存できる桁数に限りがあります。
足し算を行った結果がそれらの桁を超えた分は無視されます。



上の計算の答えは「1 0101 0001」ですが、もし保存できる桁数が8桁の場合は
9桁目以降は無視されるので、「0101 0001」として保存されます。
※このルールは他の四則演算でも同じです。

引き算

引き算も足し算と同じで10進数の方法と同じように計算できます。



コンピュータは引き算ができません。
その為、引き算を行うために補数を使って足し算で引き算の答えを求めています。
例として「(1011)2 - (0110)2」を補数で行います。
まず、計算の答え合わせのために通常の引き算で答えを求めておきます。



補数による引き算は引く側の値(右の項)の補数を作ります。



作成した補数を使って(1011)2に足します。



計算の結果は「(1 0101)2」となりました。
この結果から計算で使用した4桁を超えた桁を削除した「(0101)2」が答えです。

きちんと引き算ができたかどうかを確かめるために
最初に行った引き算の結果と比較してみます。

同じ結果になってるので、補数を使用した計算で引き算ができていることが分かります。

掛け算

掛け算も10進数の方法と同じように計算できます。



コンピュータの掛け算は掛ける数(右の項)だけ掛けられる数(左の項)を足し算します。



掛ける数が大きいとその分足し算の回数が増えてしまうので、
計算量を減らすために、シフト演算を使って計算をしています。
この計算は、まず掛けられる数を各桁毎に分解します。

各桁のべき乗する数だけ、掛けられる数を左シフトしますが、
シフトするのは各桁の数が0じゃない桁だけです。
また、シフトの計算は各桁ごとに行います。
つまり、3桁分あれば3回に分けてシフトします。
今回の計算で有効な桁は下位の2桁なので、2回シフト計算を行います。

このシフト演算で出た数を全て足した数が掛け算の答えです。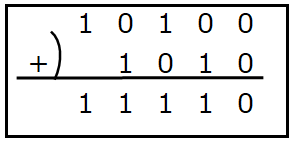

割り算

割り算も10進数の方法と同じように計算できます。



コンピュータの割り算は割られる数(左の項)が0または負の数になるまで、
割る数で引き続けます。



この時の引いた回数が割り算の答えで0または負の数が割り算のあまりです。
※余りは正の数として扱います。

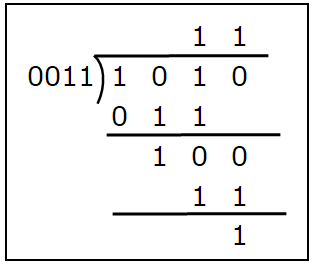
この他に、筆算と同じ方法で割り算を行う方法があります。
上位の桁から始まり、引き算ができるなら1、できないなら0として
その桁の答えを決めて、値が1なら割る数で引き算を行います。



この計算を最下位の桁まで実行し続けます。

まとめ

今回の記事の要点を最後にまとめました。