2Dの線分と線分の当たり判定

概要

最終更新日：2022/01/24

2Dの線分と線分の当たり判定について書いた記事です。
主に以下の内容を知りたい方に向けて書いています。

注意点

この記事内の座標軸はX軸「右が正、左が負」Y軸「下が正、上が負」で書いています。

サンプル

サンプルはここからダウンロードでき、環境については以下の内容となっています。


	
開発環境
	

		
VSのバージョン
		
VisualStudio 2019
	
	

		
DirectXのバージョン
		
DirectX9
	

判定方法

線分と線分の当たり判定は線分が交差していたら当たっていると判定します。
これは2Dでも3Dでも同じです。
では、交差判定はどうすればいいかというと、複数の方法があります。
今回の記事ではその中の外積を使用した方法で交差判定を行いたいと思います。

2Dの外積の特性

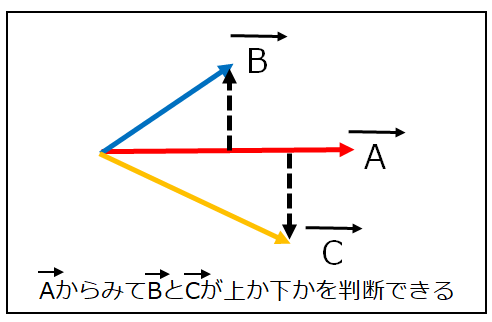
2Dのベクトルで外積計算を行うと外積のベクトルのZ成分がそのままベクトルの大きさとして使えます。
そして、その大きさは符号付きの大きさになっており、その情報を使うことで
片方のベクトルがもう一つのベクトルの左右(上下)のどちらにあるかを判断することが出来ます。



	

		
計算結果
		
方向
	
	

		
負の値
		
上(左)
	
	

		
正の値
		
下(右)
	

上の表とは異なり、上(左)が正の値とされていることもありますが、これは座標系の問題です。
DirectXは左手系なので、始点のベクトルから下(右)にあれば正の値、上(左)にあれば負の値となります。

外積を使った判定方法

外積を使った判定では、以下の条件を満たすことで交差しているとします。

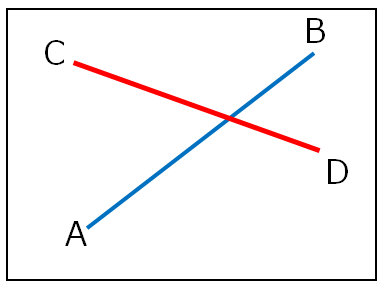上の図なら「線分ABの両端の点AとBが線分CDを、線分CDの両端の点CとDが線分ABの線を跨いだ位置にある」ため、
この二つの線分は交差していると判定します。



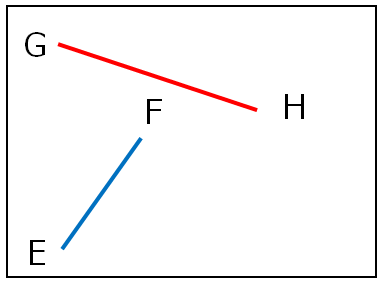上の図は線分EFの両端の点EとFが線分GHの線をまたいでいないので、交差条件を満たしていません。
そのため、交差していないと判定します。
この判定のキモとなる線分の両端の二点がもう片方の線分をまたいでいるかどうかを判断する方法として外積を使います。

判定の流れ

判定の流れは以下の通りです。

線分をベクトルにしてグループを作る

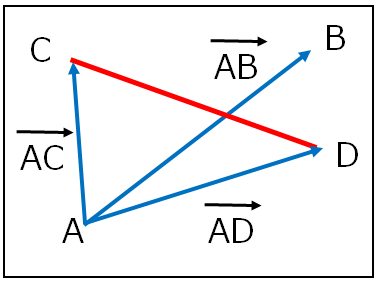
まずはこの二つ線分から以下のように三つのベクトルを持つグループを二つ作ります。

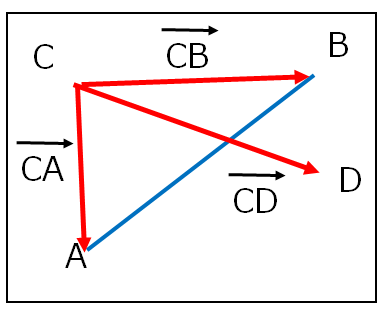
上の図からイメージが出来ると思いますが、二つの線分が交差している場合、
二つのグループの線分AB or CDのベクトルの左右に、残り二つのベクトルが存在します。
これを外積によって証明すれば、判定は完了します。

各グループのベクトルで外積計算する

各グループのベクトルを使って外積計算を行います。
ここでは、線分ABをメインで使うグループを例に説明しますが、線分CDのグループでも方法は変わりません。

外積の計算では二つのベクトルを「ベクトル① × ベクトル②」として指定します。
この時、ベクトル①の項にはグループのメインとして扱っているベクトルを使います。
今回はベクトルABがメインなので「AB × ベクトル②」になります。
ベクトル②の項には線分CDから作ったAC、またはADを設定します。
これで「AB × AC or AD」となり、外積計算をするための情報が集まったので計算を行います。



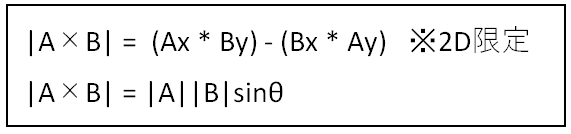上の式は外積のベクトルの長さを求める式で、最初の式は2D限定で使用できます。
今回はθを求めていないので、ベクトルの成分のみの式を使って計算します。
ACかADのどちらかの計算を行ったら、もう一つのベクトルでも同じように計算を行います。

結果が条件を満たしているかを確認する

外積計算を行ったらその結果を使い、判定を行います。
判定条件は「片方の線分の両端の点がもう片方の線分を跨いだ位置にある」です。
この条件を外積の結果で判断する場合、次のような条件式となります。

if ( (|AB × AC|) * (|AB × AD|) < 0)
{
	線分は跨いだ状態にある
}
else
{
	線分は跨いでいない
}

上の条件式のように、二つの外積の長さを乗算した結果が負の値になっているなら、
点Cと点Dは線分ABを跨いだ位置にあると判断されます。
これは2Dの外積のベクトルの長さは、左の項のベクトルから見た右の項のベクトルの位置関係が
符号によって判別できるため、その特性を利用して判断しています。


	

		
符号①
		
符号②
		
乗算結果
	
	

		
正
		
正
		
正
	
	

		
負
		
負
		
正
	
	

		
正
		
負
		
負
	
	

		
負
		
正
		
負
	

上の表から、乗算して負の値になるということは計算を行った値の符号が異なることを示しています。
今回はベクトルABを対象としてACとADで外積計算を行いました。
その結果の値の符号が異なるということは、二つのベクトルがABベクトルを挟んだ位置にあるということです。

②に戻りもう一つのグループでやり直す

ABをメインとしたグループの判定結果が条件を満たしていたら
もう一つのCDをメインとしたグループでも外積計算と条件チェックを行い、
そちらも条件を満たす結果になったのなら、二つの線分は交差していると判定します。

実装方法

実装は「判定の流れ」の順番で行っていきます。
まずは線分からベクトルの作成します。

// グループ①
Vec2 a_to_b = Vec2(line_ab.End.X - line_ab.Start.X, line_ab.End.Y - line_ab.Start.Y);
Vec2 a_to_c = Vec2(line_cd.Start.X - line_ab.Start.X, line_cd.Start.Y - line_ab.Start.Y);
Vec2 a_to_d = Vec2(line_cd.End.X - line_ab.Start.X, line_cd.End.Y - line_ab.Start.Y);

// グループ②
Vec2 c_to_d = Vec2(line_cd.End.X - line_cd.Start.X, line_cd.End.Y - line_cd.Start.Y);
Vec2 c_to_a = Vec2(line_ab.Start.X - line_cd.Start.X, line_ab.Start.Y - line_cd.Start.Y);
Vec2 c_to_b = Vec2(line_ab.End.X - line_cd.Start.X, line_ab.End.Y - line_cd.Start.Y);

ベクトルが完成したら外積計算をします。

// グループ①の外積
float d_01 = (a_to_b.X * a_to_c.Y) - (a_to_c.X * a_to_b.Y);
float d_02 = (a_to_b.X * a_to_d.Y) - (a_to_d.X * a_to_b.Y);

計算結果が出たら判定します。

// 乗算結果が正なので始点と終点がまたがっていない
if (d_01 * d_02 > 0.0f)
{
	return false;
}

判定の条件は成功ではなく、失敗の条件に変えているので注意して下さい。
これで、グループ①の判定が完了したのでグループ②も同じように計算と判定をします。

// グループ②の外積
d_01 = (c_to_d.X * c_to_a.Y) - (c_to_a.X * c_to_d.Y);
d_02 = (c_to_d.X * c_to_b.Y) - (c_to_b.X * c_to_d.Y);

// 乗算結果が正なので始点と終点がまたがっていない
if (d_01 * d_02 > 0.0f)
{
	return false;
}

最終的に関数の最後まで来たら当たりとします。

// 当たり
return true;

これで、2Dの線分同士の当たり判定の実装は終了です。