扇形と点の当たり

概要

最終更新日：2021/12/23

扇形(円弧)と点の当たりの説明をします。
この判定の実装をするとオブジェクトに視野を持たせることが可能となります。
視野を実装することでより生物らしい動きになります。

注意点

この記事内の座標軸はX軸「右が正、左が負」Y軸「下が正、上が負」で書いています。

サンプル

サンプルはここからダウンロードでき、環境については以下の内容となっています。


	
開発環境
	

		
VSのバージョン
		
VisualStudio 2019
	
	

		
DirectXのバージョン
		
DirectX9
	
	

		
説明
		
扇と点の当たり判定を行っています
通常の点の色は白く、扇と当たっている間は赤になります。
キーボードの上下左右で点を移動できます。
キーボードのAとDで扇の範囲を変更できます。
	

判定方法

判定は以下の条件を両方とも満たしていた場合に当たっているとします。

判定手順

手順以下の通りです。

①は準備、②が二つの判定に必要な情報の用意で、
③～④が長さ判定、⑤～⑧が範囲の比較です。

準備

判定を行うためには以下の情報が必要です。

扇

点

扇と点のベクトルを求める

まずは二つの判定に共通して必要な情報である扇と点のベクトルを
以下の式を使用してを求めます。

扇と点の2点間の長さを測る

扇と点のベクトルが出たので、このベクトルの長さを以下の式を使用して求めます。

長さを比較する

扇と点の長さが分かったので扇の長さ情報と比較します。
比較は以下の条件式で行います。

条件が満たされていた場合は、点が範囲内にあるかを調べる工程に進みますが、
満たされていなかった場合は、ここで判定を終了します。

扇の方向ベクトルを求める

扇の方向ベクトルは方向のベクトルが分かっている場合は三角関数を使用して求めます。
もし、カメラの中心点と注視点のように二つの座標が分かっているなら、座標からベクトルを求めても大丈夫です。
※求めたベクトルは必ず単位ベクトルにしてください。



扇の範囲はこのベクトルを扇の中心線として範囲の角度を2等分した形で展開します。

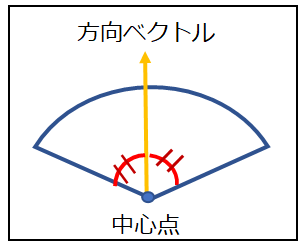
二つのベクトルの内積を求める

上で求めた二つのベクトルの成分を使用して内積計算を行います。
※扇と点のベクトルも単位ベクトルにします。

どちらのベクトルも単位ベクトルだった場合、以下のように計算結果がそのままなす角(cosθ)となります。

もし、単位ベクトルではなかった場合は、なす角(cosθ)を求めてください。

扇の範囲からcosの値を求める

上の内積結果と比較するため扇の範囲を示す角度からcosの値を求めます。
この時、角度は1/2にしてください。

なぜ1/2にするのかというと、扇の中心線である方向ベクトルを始線(0度)として扇は展開をしています。
その場合、展開された扇は始線から角度 / 2の動径として展開されるため、角度を1/2にしています。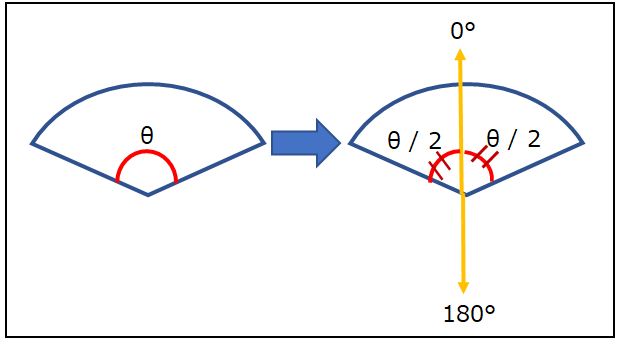

範囲を比較する

二つの角度情報が集まったので比較を行います。
比較は以下のどちらかの条件で行い、これが満たされたら点は扇の範囲内にあると考えます。

今回の範囲の判定が満たされていた場合、既に長さの判定は済ませているので
扇と点は当たっていると考えます。
逆に条件が満たされていない場合は当たっていません。

実装

サンプルの判定部分の説明をします。

準備

「1．準備」で書いてある情報は構造体を用意しました。

// 点
struct Point
{
	Vec2 position;		// 座標
};

// 扇
struct Fan
{
	Vec2 position;		// 中心座標
	float rangeDegree;	// 範囲(角度)
	float length;		// 長さ
	float directionDegree;	// 方向(角度)
};

2点間のベクトル

二つの判定で必要な扇と点のベクトルを求めます。

// 点と扇のベクトル
Vec2 vec_fan_to_point = {
	point.X - fan.Position.X,
	point.Y - fan.Position.Y
};

長さ判定

「2点間のベクトル」で求めたベクトルの長さを求めます。

// ベクトルの長さの算出
float vec_length = sqrtf((vec_fan_to_point.X * vec_fan_to_point.X) + (vec_fan_to_point.Y * vec_fan_to_point.Y));

ベクトルの長さがでたので、扇の長さと比較し、ベクトルの方が長かった場合は判定を終了します。

// ベクトルと扇の長さの比較
if (fan.Length < vec_length)
{
	// 当たっていない
	return false;
}

上記の条件が成立している状態は以下のようなイメージです。



点が扇の範囲の中に存在しないことがわかります。

範囲判定

範囲判定をおこなうために、扇の方向ベクトルを求めます。
ベクトルは三角関数を使用して求めます。

// 扇を2等分する線のベクトルを求める
float direction_rad = D3DXToRadian(fan.directionDegree);
Vec2 fan_dir = Vec2(cosf(direction_rad), sinf(direction_rad));

点と扇のベクトルと扇の方向ベクトルが分かったので二つのベクトルを使用して内積を求めますが、
その前に点と扇のベクトルは単位ベクトルにしておきます。

// 扇と点のベクトルを単位ベクトルにする
Vec2 normal_fan_to_point = {
	vec_fan_to_point.X / vec_length,
	vec_fan_to_point.Y / vec_length
};

これでどちらのベクトルも単位ベクトルとなったので、成分を使用した式で内積を求めます。

// 内積計算
float dot = normal_fan_to_point.X * fan_dir.X + normal_fan_to_point.Y * fan_dir.Y;

内積(cosθ)が求まったので、扇の範囲もcosの値にします。
※範囲を2で割ることを忘れないでください。

// 扇の範囲をcosにする
float fan_cos = cosf(D3DXToRadian(fan.rangeDegree / 2.0f));

これで範囲比較をするための情報が集まったので比較を行います。

// 点が扇の範囲内にあるかを比較する
if (fan_cos > dot)
{
	// 当たってない
	return false;
}

上記のコードのように扇の範囲であるfan_cosの方が二つのベクトルのなす角dotよりも
大きいということは扇の範囲の方が角度が小さいことになります。
(fan_cosとdotはcosの値ですので、注意して下さい)
この条件が成立した場合のイメージは以下の図のようになっており、点が扇の範囲外にあることが分かります。



そして、この条件式が不成立なら、長さと範囲が問題ないことになるので点と扇は当たっていると判断します。