点と回転矩形の当たり
概要
点と回転矩形の当たり判定の説明をします。
この判定を実装すると傾いている矩形に対しての点の当たりが可能となります。
ゲームではマウスクリックやタップした際の座標と回転状態の矩形の判定などで使われます。
今回説明する方法は「外積を使用した方法」と「座標変換を使用する方法」の二つです。
そして最後に、両方の処理の速度を計測して比べてみたいと思います。
注意点
この記事内の座標軸はX軸「右が正、左が負」Y軸「下が正、上が負」で書いています。
サンプル
サンプルはここからダウンロードでき、環境については以下の内容となっています。
開発環境
| VSのバージョン |
VisualStudio 2019 |
| DirectXのバージョン |
DirectX9 |
サンプルコードは説明をするために細かく分けていますが、実際はもっと省略して書きます。
外積を使用した方法
二次元のベクトルの外積の結果を利用すると上下判定を行うことができます。
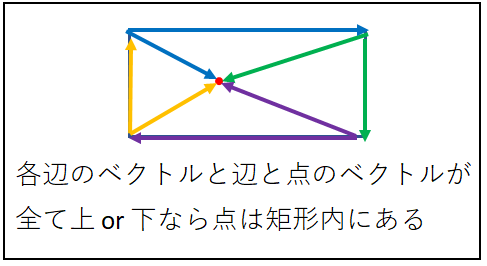
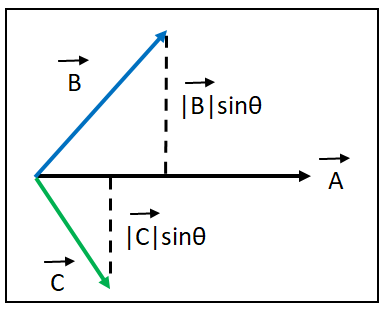 この性質を利用して「矩形の各辺のベクトルと点と辺のベクトルが
全て上、または下にあれば点は矩形内にある」と判定します。
※上か下というのはベクトルの作成方法や2DのY軸の方向で変わります。
この性質を利用して「矩形の各辺のベクトルと点と辺のベクトルが
全て上、または下にあれば点は矩形内にある」と判定します。
※上か下というのはベクトルの作成方法や2DのY軸の方向で変わります。
注意点
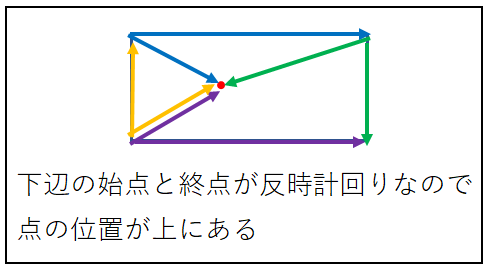
この判定方法の注意点は以下の二点です。
①.各辺のベクトルの始点は特定の頂点から
頂点までの方向を時計回りか反時計回りで固定する |
| ②.辺と点のベクトルは①のベクトルの始点から点のベクトルにする |
| ③.外積の計算順番も「辺の始点 => 辺の終点 × 辺の始点 => 点」で統一する |
この注意点を守らないと判定が成立しないので、気を付けてください。
判定の流れ
判定は以下の流れで行います。
| ①.回転矩形を用意する |
| ②.矩形の各辺の始点と終点のベクトルを用意する |
| ③.②のベクトルと始点=>点のベクトルで外積計算をする |
| ④.上下判定をする |
| ⑤.③と④を辺の数だけ繰り返す |
①.回転矩形を用意する
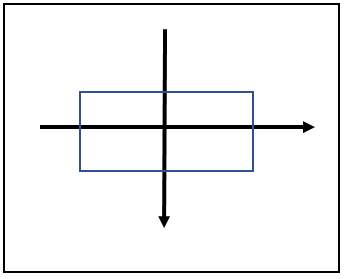
まずは矩形を回転させます。
矩形の回転は原点中心の回転を行う必要があるので
矩形のサイズ情報をもとにして原点中心の矩形を作ります。
 次に回転を行いますが、回転は各頂点に対して以下の計算式をあてはめます。
※sinの計算部分は本来Xが正でYが負ですが、
今回のY軸は上が負で下が正なので符号を反転しています。
次に回転を行いますが、回転は各頂点に対して以下の計算式をあてはめます。
※sinの計算部分は本来Xが正でYが負ですが、
今回のY軸は上が負で下が正なので符号を反転しています。
 これで回転矩形が完成します。
これで回転矩形が完成します。
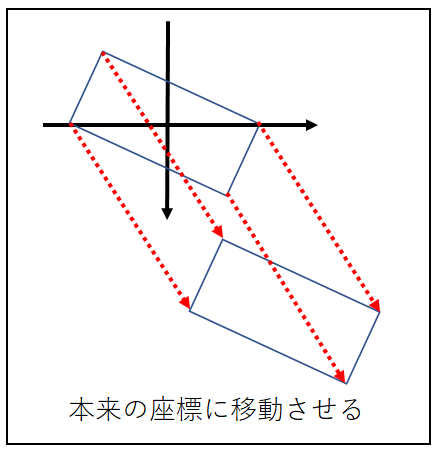
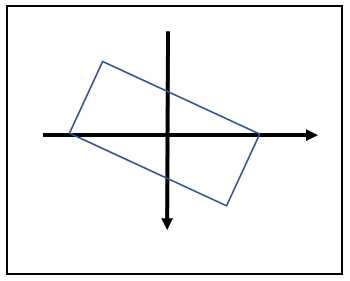 完成した回転矩形を本来の位置に移動させます。
回転矩形の各頂点に判定を行う座標にある矩形の中心座標を足すだけです。
完成した回転矩形を本来の位置に移動させます。
回転矩形の各頂点に判定を行う座標にある矩形の中心座標を足すだけです。
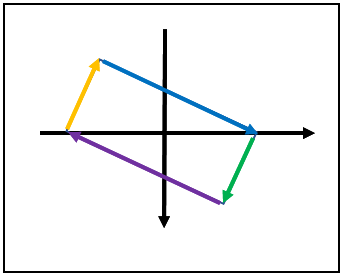
②.矩形の各辺の始点と終点のベクトルを用意する
回転矩形が用意出来たら、各辺の始点と終点をベクトル化します。
※ベクトルで使用する頂点の始点と終点の方向に注意してください。
③.②のベクトルと始点=>点のベクトルで外積計算をする
ベクトルが用意出来たらベクトルの始点と点のベクトルを作成します。
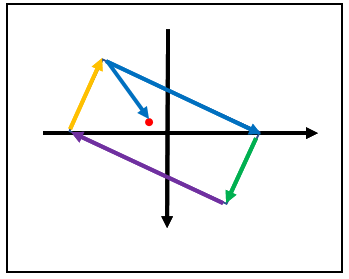 この二つのベクトルの外積を計算します。
この二つのベクトルの外積を計算します。
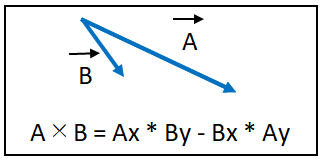
④.上下判定をする
③の外積の結果が正の値なら点は下、負の値なら点は上にあると判定します。

⑤.③と④を辺の数だけ繰り返す
③と④を全ての辺に対して行い、全ての外積結果が正ならば「矩形内に点がある」
一つでも負の値があれば「矩形の外に点がある」と判定します。
実装方法
判定の流れを順番に行えば実装できます。
まずは、①の回転矩形を用意します。
// 原点中心の矩形
Vec2 base_positions[4] =
{
Vec2(-rect.Width / 2.0f, -rect.Height / 2.0f),
Vec2(rect.Width / 2.0f, -rect.Height / 2.0f),
Vec2(rect.Width / 2.0f, rect.Height / 2.0f),
Vec2(-rect.Width / 2.0f, rect.Height / 2.0f),
};
// 矩形の中心座標
Vec2 rect_center = Vec2(rect.X + rect.Width / 2.0f, rect.Y + rect.Height / 2.0f);
// 度数法 => 弧度法変換
float rad = D3DXToRadian(degree);
// 回転矩形座標用
Vec2 vertices[4];
// 回転計算
for (int i = 0; i < 4; i++)
{
vertices[i].X = base_positions[i].X * cosf(rad) + base_positions[i].Y * -sinf(rad) + rect_center.X;
vertices[i].Y = base_positions[i].X * sinf(rad) + base_positions[i].Y * cosf(rad) + rect_center.Y;
}
次に②の矩形のベクトルを用意します。
// 矩形の4頂点から辺を作る
Edge edges[4] =
{
// Edge(始点座標, 終点座標)
Edge(vertices[0], vertices[1]), // 上辺
Edge(vertices[1], vertices[2]), // 右辺
Edge(vertices[2], vertices[3]), // 下辺
Edge(vertices[3], vertices[0]), // 左辺
};
ベクトルの用意が終わったら③を行いますが、コードの性質上③~⑤を全てのせます。
for (Edge& start_to_end : edges)
{
// 辺の始点と点で辺を作成
Edge start_to_point = Edge(start_to_end.Start, point_pos);
// 二つの辺のベクトルを取得
Vec2 vector01 = start_to_end.Vector();
Vec2 vector02 = start_to_point.Vector();
// 外積計算
float cross = vector01.X * vector02.Y - vector02.X * vector01.Y;
// 結果が負の場合点が上にあるので判定終了
if (cross < 0)
{
return false;
}
}
// 全ての外積結果が下になったので点は矩形の中にある
return true;
これで点と回転矩形の外積を使用した判定は終了です。
座標変換を使用する方法
座標変換方法は回転した矩形の中心を座標軸の原点として扱い、
判定を行う点の座標もその原点に中心の座標に変換します。
こうすることで、点も回転矩形と同じ座標軸の座標に置かれることになるので、
通常の点と矩形の判定と同じやり方で判定ができます。
流れ
以下の流れで行います。
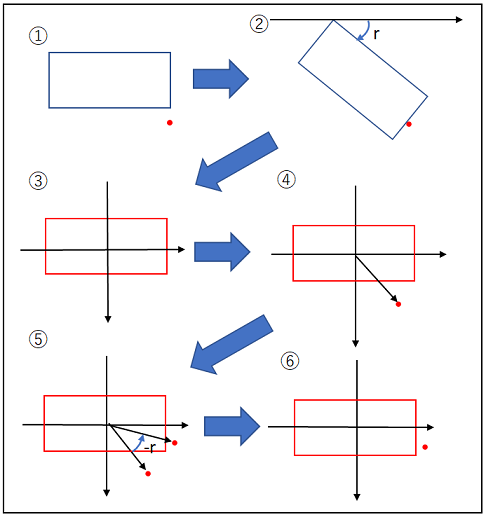
| ①.矩形と点を用意する |
| ②.矩形を回転させる |
| ③.矩形の中心を原点として扱う |
| ④.点の座標を矩形との相対座標にする |
| ⑤.点を座標変換する |
| ⑥.矩形と点の当たり判定をする |
以下の項目で説明をしていきますが、①は説明する必要もなく、
②は「外積を使用した方法」で説明しているので省略します。
③.矩形の中心を原点として扱う
矩形の中心を原点として扱いますが、その場合は矩形の移動や回転、拡縮は
全てリセットされた状態になります。
以下の表や絵を見てもらうと分かりやすいと思います。
| 座標 |
(x, y) = (0, 0) |
| 回転 |
0度 |
| 拡縮 |
(x, y) = (1, 1) |
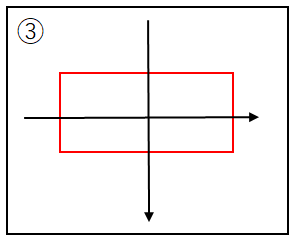
原点は
そこが中心であり、回転や拡縮の基準となるので、
座標は0や角度は0、拡縮は等倍の1です。
④.点の座標を矩形との相対座標にする
矩形の準備ができたので、次は点を変更していきます。
まずは、点の座標を2Dのワールド座標軸から矩形の座標軸の座標に変換します。
このような特定の座標を原点とした座標を「相対座標」と呼びます。
相対座標は以下の計算で算出できます。

⑤.点を座標変換する
③で作成した相対座標は回転の計算を行っていないので、判定情報として不十分です。
判定で使用するために「2Dのワールド座標軸から矩形が原点の座標軸に変換」を行います。
では、変換をどう行えばよいかというと矩形がワールド座標軸上で行った、
座標に関する計算の反対の事を行います。
これは③の項目の説明の「移動や回転、拡縮は全てリセット」に関する部分です。
例えば、矩形のワールド座標軸上での座標情報が以下の内容だったします。
| 座標 |
(x, y) = (200, 100) |
| 回転 |
30度 |
| 拡縮 |
(x, y) = (3, 4) |
これを原点として扱うためには以下の計算をする必要があります。
| 座標 |
(x, y) = (-200, -100) |
| 回転 |
-30度 |
| 拡縮 |
(x, y) = (1 / 3, 1 / 4) |
上の二つの表で計算すると全てリセットされて原点と同じ状態になります。
そして、これらの計算を一度にまとめて行う方法として逆行列があります。
逆行列は「
行列とその逆行列を掛けると単位行列になる性質」を持っており、
単位行列は行列の初期状態を表します。
つまり、行列の成分を全てリセットするということです。
この性質を利用して計算を行いますが、今回は説明を分かりやすくするために
③で点と矩形の相対座標を用意して、移動情報を行列から外しています。
今回は足らない情報である回転のみの逆行列を作成します。
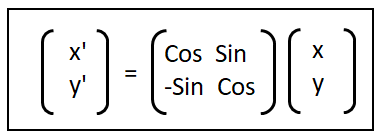
この逆行列を点の座標に反映したら矩形が原点に変換するために行われた計算が
反映されることになるので、点の座標軸がワールドから矩形に変換されます。
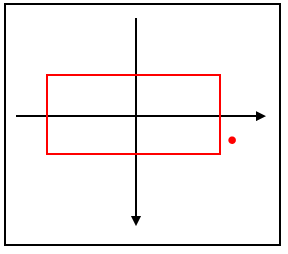
⑥.点と矩形の当たり判定を行う
最後に点と矩形の判定を行いますが、以下のように矩形も点も
同じ座標軸に回転を行っていない状態で配置されているので、
通常の点と矩形の判定で問題ありません。
実装方法
実装は流れの内容を順番に実装していきます。
①~③までは実装の必要がなかったり、説明済みなので④から実装を行います。
④の点と矩形の相対座標を求める処理は説明で書いていた式にあてはめるだけです。
// 矩形の中心を原点とした相対座標を作成する
Vec2 relative_position = Vec2(point_pos.X - rect_center.X, point_pos.Y - rect_center.Y);
⑤の実装は矩形のワールド座標上での回転情報を打ち消すための
逆行列を作成して、それを③の相対座標に反映します。
// 相対座標に対して矩形の回転を打ち消す逆行列を掛ける
Vec2 transform_pos = Vec2(
cosf(rad) * relative_position.X + sinf(rad) * relative_position.Y,
-sinf(rad) * relative_position.X + cosf(rad) * relative_position.Y
);
これで点の座標変換が完了したので、あとは⑥の矩形と点の当たり判定を行うだけです。
この判定では、わざわざ元の座標に戻す必要はなく、中心が原点にある矩形と
点の当たり判定を行えば問題ありません。
// 矩形と点の当たり判定を行う
if (-rect.Width / 2.0f <= transform_pos.X && rect.Width / 2.0f >= transform_pos.X &&
-rect.Height / 2.0f <= transform_pos.Y && rect.Height / 2.0f >= transform_pos.Y)
{
return true;
}
これで座標変換による当たり判定が完成しました。
速度比較
当たり判定は処理コストが低い方が有利なので、
今回説明した二つの方法の速度比較をしてみたいと思います。
// 計測開始
QueryPerformanceCounter(&s);
for (int i = 0; i < 1000; i++)
{
if (IsCollidingCoordinateTransformVersion(rect, degree, GetMousePos()) == true)
{
is_colliding = true;
}
else
{
is_colliding = false;
}
}
// 計測終了
QueryPerformanceCounter(&e);
// 出力
process_time = (double)(e.QuadPart - s.QuadPart) / f.QuadPart;
str = "座標変換版:" + std::to_string(process_time) + "\n";
OutputDebugString(str.c_str());
// 計測開始
QueryPerformanceCounter(&s);
for (int i = 0; i < 1000; i++)
{
if (IsCollidingCrossVersion(rect, degree, GetMousePos()) == true)
{
is_colliding = true;
}
else
{
is_colliding = false;
}
}
// 計測終了
QueryPerformanceCounter(&e);
// 出力
process_time = (double)(e.QuadPart - s.QuadPart) / f.QuadPart;
str = "外積版:" + std::to_string(process_time) + "\n";
OutputDebugString(str.c_str());
実行結果:
座標変換版:0.000193
外積版:0.001158
上の結果の通り、座標変換版が圧倒的に高速でした。
二つの判定は方法は最適化をしていないので、この結果が全てではありませんが、
この速度差は覆しにくいと思うので座標変換版の方法を使用した方がいいと思います。
この性質を利用して「矩形の各辺のベクトルと点と辺のベクトルが 全て上、または下にあれば点は矩形内にある」と判定します。 ※上か下というのはベクトルの作成方法や2DのY軸の方向で変わります。


次に回転を行いますが、回転は各頂点に対して以下の計算式をあてはめます。 ※sinの計算部分は本来Xが正でYが負ですが、 今回のY軸は上が負で下が正なので符号を反転しています。
これで回転矩形が完成します。
完成した回転矩形を本来の位置に移動させます。 回転矩形の各頂点に判定を行う座標にある矩形の中心座標を足すだけです。


この二つのベクトルの外積を計算します。



 原点はそこが中心であり、回転や拡縮の基準となるので、
座標は0や角度は0、拡縮は等倍の1です。
原点はそこが中心であり、回転や拡縮の基準となるので、
座標は0や角度は0、拡縮は等倍の1です。

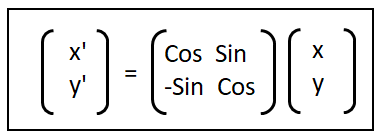 この逆行列を点の座標に反映したら矩形が原点に変換するために行われた計算が
反映されることになるので、点の座標軸がワールドから矩形に変換されます。
この逆行列を点の座標に反映したら矩形が原点に変換するために行われた計算が
反映されることになるので、点の座標軸がワールドから矩形に変換されます。


