Top プログラム言語 概論 アルゴリズム
コンピュータ基礎 ゲーム ゲームAI 当たり判定
デバッグ モデル描画 Unity Unity初心者
ツール シェーダ UML ハードウェア
数学 DirectX Git モバイル
ネットワーク CG 　 　
プライバシーポリシー 当サイトについて お問い合わせ 　


矩形と矩形の当たり

目次


概要

矩形と矩形の当たり判定は円と円の当たり判定と同じくらいよく使用される判定方法です。
2Dゲームで描画するオブジェクトのほとんどが矩形で描画されます。
そのことから「描画範囲 = 当たり範囲」とすることが可能なので
初心者が実装する当たり判定の方法として使いやすくなっています。
この判定でよく使われる判定方法は「距離を使用する方法」と
「辺の位置関係を使用する方法」があります。

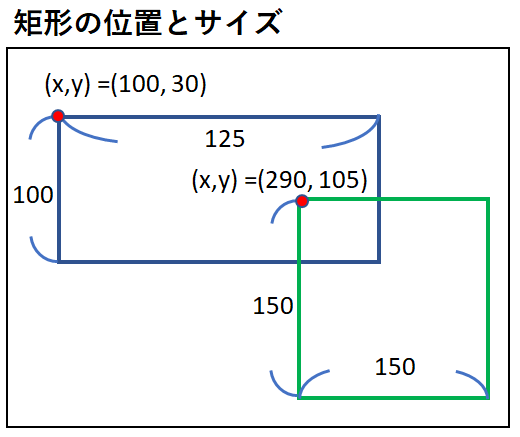collision_0025

今回判定に使用する矩形の関係、サイズは上の図の内容で行います。

注意点

この記事内の座標軸はX軸「右が正、左が負」Y軸「下が正、上が負」で書いています。

サンプル

サンプルはここからダウンロードでき、環境については以下の内容となっています。



	開発環境
	

		VSのバージョン
		DirectXのバージョン
	

	

		VisualStudio 2019
		DirectX9
	



サンプルコードは説明をするために細かく分けていますが、実際はもっと最適化します。

矩形

矩形とは全ての角が直角(90度)の四角形(長方形)のことです。

common_0001

矩形の作り方

４つの点の内で対角の２点の座標を用意することが出来たら矩形の作成ができます。
※これ以降で紹介する計算はX軸は右が正で左が負、
　Y軸は下が正で上が負の座標軸で行っています。

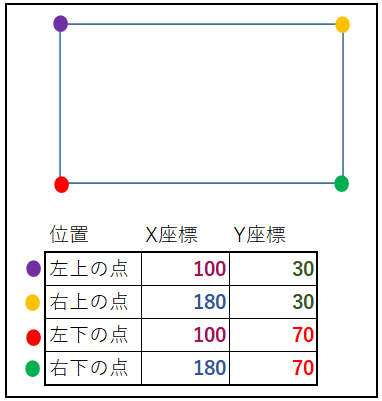common_0002

上図の矩形の座標でわかるように左上と右下、右上と左下などの
対角の点の座標が分かれば残りの点の座標の割り出しができます。

矩形の点は矩形の原点座標と矩形の縦と横のサイズから割り出すことができ、
原点座標は「左上」「中央」「中央下」のいずれかにすることが多いです。

左上

左上はDirectXなどを使用したプログラムで多く使用される原点の位置です。

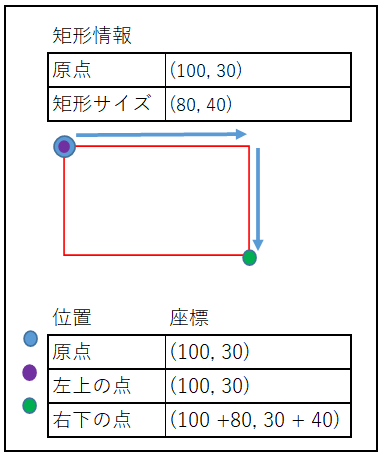common_0003

原点が左上の場合、そのまま左上を２点の内の１点として扱い、
もう１点は対角の右下となります。
右下の点は原点である左上の座標に矩形のサイズを足すことで割り出せます。

float x = 100.0f;
float y = 30.0f;
float width = 80.0f;
float height = 40.0f;

printf("左上座標 (x, y) = (%.1f, %.1f)\n", x, y);
printf("右下座標 (x, y) = (%.1f, %.1f)\n", x + width, y + height);


// 実行結果
左上座標 (x, y) = (100.0f, 30.0f)
右下座標 (x, y) = (180.0f, 70.0f)

中央

中央の場合は対角となる２点を決めてから割り出しを行います。
DirectXなどでは左上と右下の２点で行うことが多いので、
今回はそちらの２点を使用した説明をします。

common_0004

原点が中央の場合は、矩形のサイズを２で割った結果を使用します。
結果の反映は左上の場合はX、Yともに原点から引いて、
右下の場合は原点から足します。

float x = 100.0f;
float y = 30.0f;
float width = 80.0f;
float height = 40.0f;

float half_width = width / 2.0f;
float half_height = height / 2.0f;

printf("左上座標 (x, y) = (%.1f, %.1f)\n", x - half_width, y - half_height);
printf("右下座標 (x, y) = (%.1f, %.1f)\n", x + half_width, y + half_height);


// 実行結果
左上座標 (x, y) = (60.0f, 10.0f)
右下座標 (x, y) = (140.0f, 50.0f)

中央下

中央下の場合も対角となる２点を決めてから割り出しを行うので、
中央と同じで左上と右下の２点を使用した説明をします。

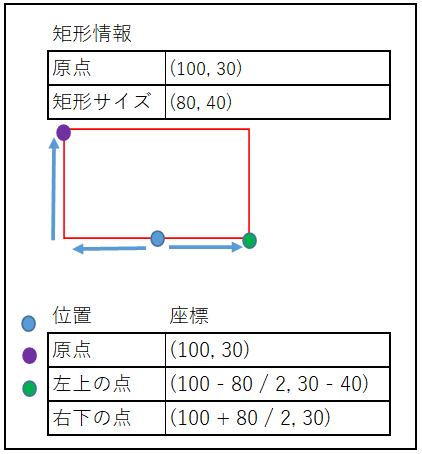common_0005

中央下の場合X軸は矩形のサイズを２で割った値を
左の点は原点から引いて、右の点は原点から足します。
Y軸は上の点は原点から縦のサイズ分だけ引いて、
下の点は原点の値をそのまま使用します。

float x = 100.0f;
float y = 30.0f;
float width = 80.0f;
float height = 40.0f;

float half_width = width / 2.0f;

printf("左上座標 (x, y) = (%.1f, %.1f)\n", x - half_width, y - height);
printf("右下座標 (x, y) = (%.1f, %.1f)\n", x + half_width, y);


// 実行結果
左上座標 (x, y) = (60.0f, -10.0f)
右下座標 (x, y) = (140.0f, 30.0f)

距離を使用する方法

距離を使用する方法は２つの矩形の座標のX軸、Y軸に対して別々に距離を測り、
その距離を２つの矩形の長さ(XとYは別)の和と比較して、和の方が小さい値なら当たり、
大きければ当たってないと判定します。

判定方法

判定の流れは以下の流れで行います。
※各項目コード付きで説明していますが、
　このコードはサンプルのものを使っています。



	

		 順番 
		 内容 
	

	

		 ① 
		 矩形の中心座標を算出する 
	

	

		 ② 
		 X軸、Y軸の距離を算出する 
	

	

		 ③ 
		 ２つの矩形のX軸、Y軸のサイズの和を算出する 
	

	

		 ④ 
		 サイズの和と距離を比較する 
	



②と③の順番は前後しても問題ありません。

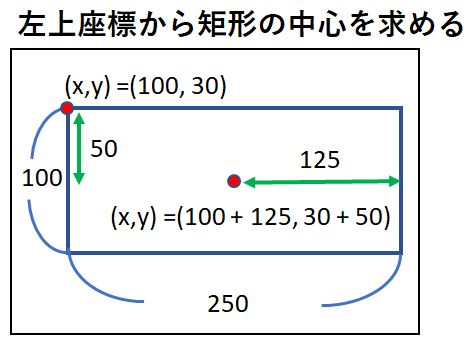
①．矩形の中心座標を算出する

この項目は矩形の座標の原点をどの位置で行っているかによって
そのまま②に移動して問題ありません。
対象は「中心以外の位置が原点」の場合で「左上」「中下」などです。

DirectXなどでは矩形は描画開始位置である左上が
そのまま使われていることがありますので、
そのような場合はこの項目で中心座標の算出を行ってください。
算出方法
算出はどの位置を原点にしているのかを理解していれば簡単です。
その原点から中心に座標を移動させるための値を割り出して足し算するだけです。
今回は左上が原点の場合の説明をします。
左上からみた中心座標は矩形の縦と横のサイズを２で割った値を足せばでます。

collision_0016
実装方法
/*
	使用している構造体
		
	Rect
		float型４つある構造体
		座標(X、Y)とサイズ(Width、Height)
	
	Vec2はfloat型が２つある構造体
		座標(X、Y)
*/

// 矩形の中心座標を割り出す(座標原点は左上)
Vec2 center_a = { 
	rect_a.X + (rect_a.Width / 2.0f), 
	rect_a.Y + (rect_a.Height / 2.0f)
};
Vec2 center_b = {
	rect_b.X + rect_b.Width / 2.0f,
	rect_b.Y + rect_b.Height / 2.0f
};

②．X軸、Y軸の距離を算出する

中心座標の算出が完了したら、２つの矩形の距離を測ります。
この時は「座標間の距離」を測るのではなく
「X座標間の距離」と「Y座標間の距離」を別々に測ります。
算出方法
算出方法は単純で２つの矩形座標の各軸の座標同士で引き算を行います。
距離は絶対値として扱う必要があるので計算結果が負の値なら
-1を掛けて正の値にします。
※各言語には値を絶対値にしてくれる関数があるので
　そちら使った方がコードがシンプルになります。

collision_0017
実装方法
/*
	使用している構造体
		
	Vec2はfloat型が２つある構造体
		座標(X、Y)
*/
// 距離を割り出す
Vec2 distance = {
	center_a.X - center_b.X,
	center_a.Y - center_b.Y
};

if (distance.X < 0.0f)
{
	distance.X *= -1.0f;
}

if (distance.Y < 0.0f)
{
	distance.Y *= -1.0f;
}

③．２つの矩形のX軸、Y軸のサイズの和を算出する

次は２つ矩形のX軸、Y軸のサイズの和を２で割った値を使用します。

collision_0018
実装方法
/*
	使用している構造体
		
	Vec2はfloat型が２つある構造体
		座標(X、Y)
*/
// サイズの和を割り出す
Vec2 size_sum = {
	(rect_a.Width + rect_b.Width) / 2.0f,
	(rect_a.Height + rect_b.Height) / 2.0f
};

④．サイズの和と距離を比較する

最後に②と③の情報を使用して比較を行います。
その結果、以下の条件を全て満たした場合、当たっていると判断します。



	 条件 
	

		 X軸の距離がX軸のサイズの和よりも小さい or 以下 
	

	

		 Y軸の距離がY軸のサイズの和よりも小さい or 以下
証明
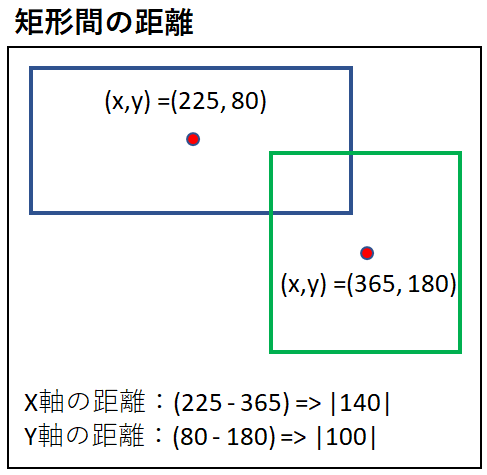
下の図の情報を整理して当たっていることを証明します。

collision_0019

まず、矩形間の距離はこのようになります。


	 距離 
	

		 軸 
		 距離 
	

	

		 X軸 
		 225 - 265 => |140| 
	

	

		 Y軸 
		 80 - 180 => |100| 
	



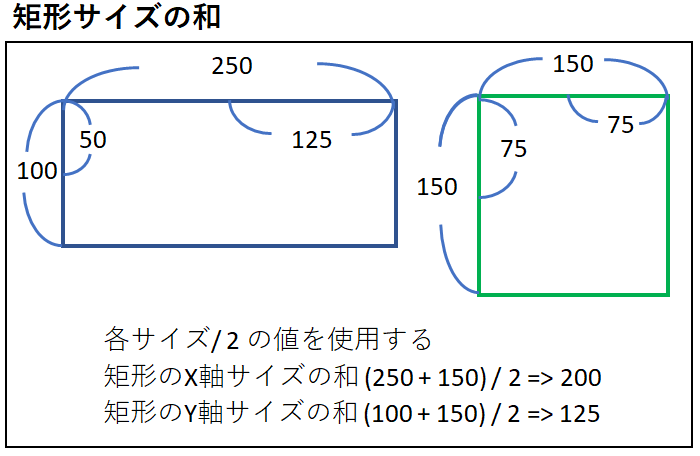
次に２つの矩形のサイズはこの通りです。


	 サイズ 
	

		 軸 
		 サイズ 
	

	

		 X軸 
		 125 + 75 => 200 
	

	

		 Y軸 
		 50 + 75 => 125 
	



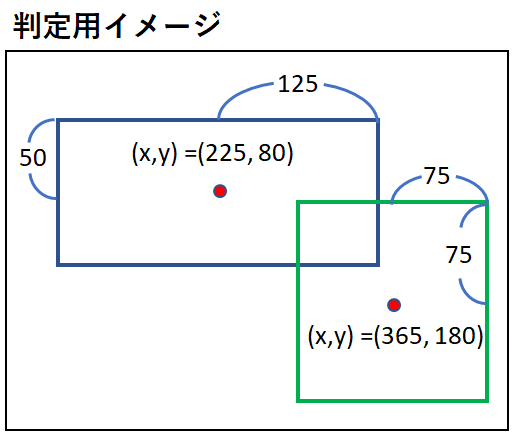
距離とサイズの情報を使って当たっているかの判定をします。


	 判定 
	

		 軸 
		 式(距離 < サイズ) 
		 結果 
	

	

		 X軸 
		 140 < 200 
		 成立してる 
	

	

		 Y軸 
		 100 < 125 
		 成立してる 
	



X軸、Y軸の条件はどちらも成立しているので
この矩形同士の当たりは当たっていると判断できます。
実装方法
/*
	使用している構造体
		
	Vec2はfloat型が２つある構造体
		座標(X、Y)
*/
// 判定(距離 < サイズの合計なら当たり)
if (distance.X < size_sum.X &&
	distance.Y < size_sum.Y)
{
	return true;
}

辺の位置関係を使用する方法

辺の位置関係を使用する方法は矩形の「左辺」「右辺」「上辺」「下辺」の
４辺の位置関係から２つの矩形が当たっているかどうかを判断します。

判定方法

判定の流れは以下の流れで行います。
※各項目コード付きで説明していますが、
　このコードはサンプルのものを使っています。



	

		順番
		内容
	

	

		 ① 
		 対角線上の頂点座標を求める 
	

	

		 ② 
		 矩形Aの左辺と矩形Bの右辺の位置関係を調べる 
	

	

		 ③ 
		 矩形Aの右辺と矩形Bの左辺の位置関係を調べる 
	

	

		 ④ 
		 矩形Aの上辺と矩形Bの下辺の位置関係を調べる 
	

	

		 ⑤ 
		 矩形Aの下辺と矩形Bの上辺の位置関係を調べる 
	

	

		 ⑥ 
		 判定 
	



②～⑤の順番は前後しても問題ありません。

①．対角線上の頂点座標を求める

矩形の各辺の情報を知るためには対角線上にある２頂点を求める必要があります。
矩形を作成するための原点となる座標があるはずなので、
そちらを利用して頂点を算出します。
今回の例では矩形の原点座標は左上として考えています。

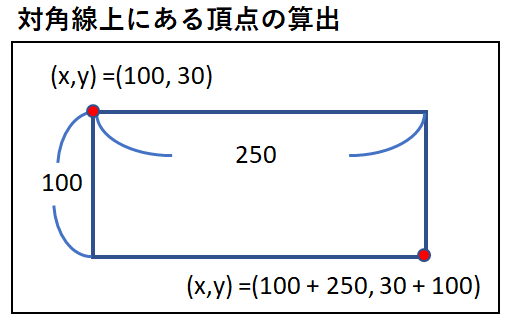collision_0020

原点を左上座標とした場合、既に左上座標が分かっているので
右下座標を算出するだけです。
右下座標は左上座標に矩形サイズを加算することで求められます。



	頂点情報
	

		 位置 
		 座標 
	

	

		 原点 
		 (x, y) = (100, 30) 
	

	

		 左上 
		 (x, y) = (100, 30) 
	

	

		 右下 
		 (x, y) = (100 + 250, 30 + 100)
実装方法
/*
	使用している構造体

	Rect
		float型４つある構造体
		座標(X、Y)とサイズ(Width、Height)

	Vec2はfloat型が２つある構造体
			座標(X、Y)
*/
// 矩形の左上、右下座標の算出
Vec2 a_left_top = {
	rect_a.X,
	rect_a.Y
};

Vec2 a_right_bottom = {
	rect_a.X + rect_a.Width,
	rect_a.Y + rect_a.Height
};

Vec2 b_left_top = {
	rect_b.X,
	rect_b.Y
};

Vec2 b_right_bottom = {
	rect_b.X + rect_b.Width,
	rect_b.Y + rect_b.Height
};

②．矩形Aの左辺と矩形Bの右辺の位置関係を調べる

矩形Aの左辺と矩形Bの右辺の位置関係では、矩形Aの左辺のX座標が
矩形Bの右辺のX座標よりも左側にある必要があり、
イメージとしては下の図のような位置関係となります。

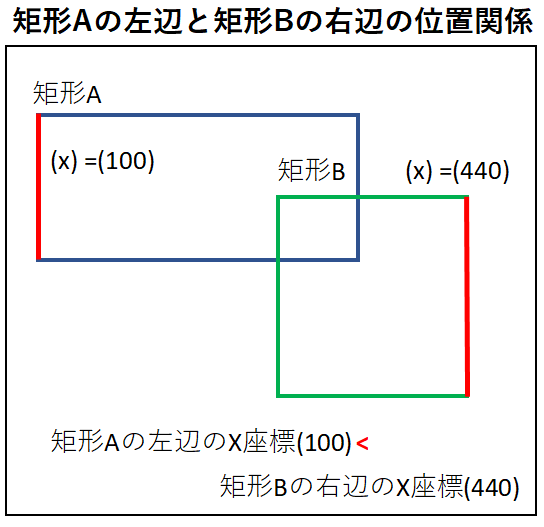
collision_0021
実装方法
/*
	使用している構造体

	Vec2はfloat型が２つある構造体
			座標(X、Y)
*/
// 矩形Aの左辺と矩形Bの右辺の関係チェック
bool is_left_less_right = false;
if (a_left_top.X <= b_right_bottom.X)
{
	is_left_less_right = true;
}

③．矩形Aの右辺と矩形Bの左辺の位置関係を調べる

矩形Aの右辺と矩形Bの左辺の位置関係では、矩形Aの右辺のX座標が
矩形Bの左辺のX座標よりも右側にある必要があり、
イメージとしては下の図のような位置関係となります。

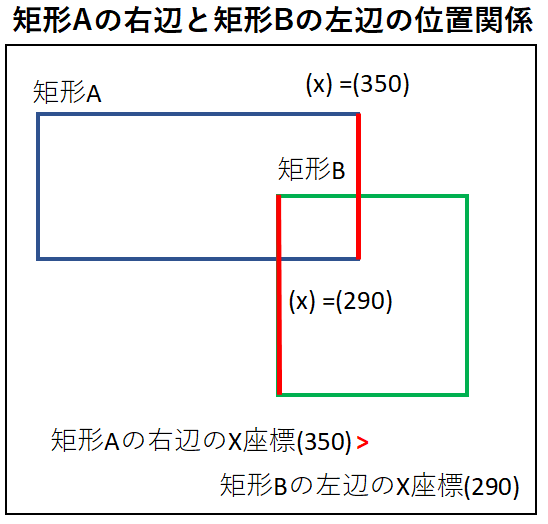
collision_0022
実装方法
/*
	使用している構造体

	Vec2はfloat型が２つある構造体
			座標(X、Y)
*/
// 矩形Aの右辺と矩形Bの左辺の関係チェック
bool is_right_greater_left = false;
if (a_right_bottom.X >= b_left_top.X)
{
	is_right_greater_left = true;
}

④．矩形Aの上辺と矩形Bの下辺の位置関係を調べる

矩形Aの上辺と矩形Bの下辺の位置関係では、矩形Aの上辺のY座標が
矩形Bの下辺のY座標よりも上側にある必要があり、
イメージとしては下の図のような位置関係となります。

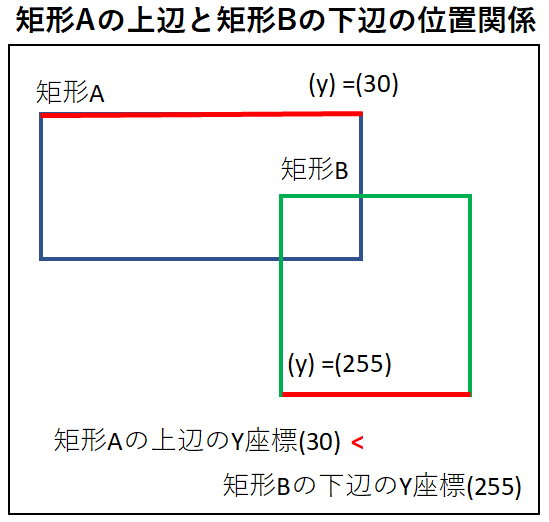
collision_0023
実装方法
/*
	使用している構造体

	Vec2はfloat型が２つある構造体
			座標(X、Y)
*/
// 矩形Aの上辺と矩形Bの下辺の関係チェック
bool is_top_less_bottom = false;
if (a_left_top.Y <= b_right_bottom.Y)
{
	is_top_less_bottom = true;
}

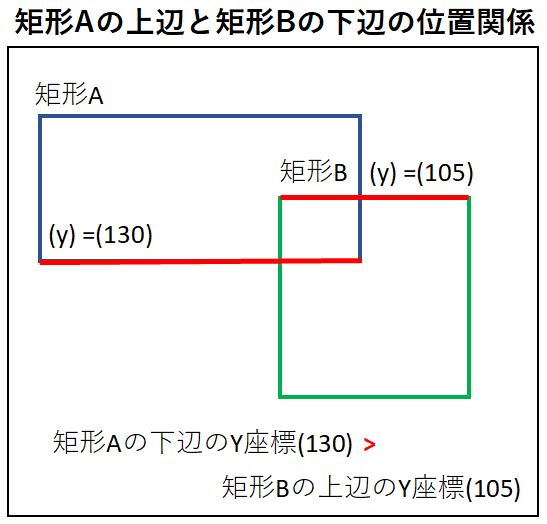
⑤．矩形Aの下辺と矩形Bの上辺の位置関係を調べる

矩形Aの下辺と矩形Bの上辺の位置関係では、矩形Aの下辺のY座標が
矩形Bの上辺のY座標よりも下側にある必要があり、
イメージとしては下の図のような位置関係となります。

collision_0024
実装方法
/*
	使用している構造体

	Vec2はfloat型が２つある構造体
			座標(X、Y)
*/
// 矩形Aの下辺と矩形Bの上辺の関係チェック
bool is_bottom_greater_top = false;
if (a_right_bottom.Y >= b_left_top.Y)
{
	is_bottom_greater_top = true;
}

⑥．判定

判定は②～⑤までの位置関係が全て成立していると当たっていると判定します。



	位置関係
	

		 辺① 
		 辺② 
		 関係 
	

	

		 矩形A左辺 
		 矩形B右辺 
		 左辺のX座標 < 右辺のX座標 
	

	

		 矩形A右辺 
		 矩形B左辺 
		 右辺のX座標 > 左辺のX座標 
	

	

		 矩形A上辺 
		 矩形B下辺 
		 上辺のY座標 < 下辺のY座標 
	

	

		 矩形A下辺 
		 矩形B上辺 
		 下辺のY座標 > 下辺のY座標
実装方法
/*
	使用している構造体

	Vec2はfloat型が２つある構造体
			座標(X、Y)
*/
// 各辺の関係をチェックする(全てtrueなら当たり)
if (is_left_less_right == true &&
	is_right_greater_left == true &&
	is_top_less_bottom == true &&
	is_bottom_greater_top)
{
	return true;
}






探している内容が見つからなかったら以下のサイトにあるかもしれません。

 GAMEWORKS LAB




© 2020 YTTM-WORK
プライバシーポリシー    当サイトについて    お問い合わせ